sakurai - modern qm

看懂了书却⑧会做题等于白看

——樱井纯，本书序言

我的量子力学学得非常不好，很多基本的东西都没有理解（讽刺的是，成绩却是最高的）。所以必须要回炉重造。

2019.8.4 更新到前两章

第一章 基本概念

从 Stern-Gerlach 实验说起。在该实验中，银原子由于带有磁矩的缘故受到磁场的偏转。可以知道，其受到的力正比于其磁矩的z分量，而制备出来的银原子没有经过任何“筛选”，因此猜测最终打在屏上应该是连续的一片。然而实际上却是两个点，对应自旋z分量为$S_z=\pm \hbar/2$。一开始，迷惑的人们管这个叫“空间量子化”（非常不恰当的名字）。这是第一个问题。

人们又做了另一个实验。在这个实验中，本来应该已经“消失”的$S_z^-$分量神秘地又出现了。这是第二个问题。

这两件事情体现了量子现象的奇特之处。基于此以及其他一些奇怪的事情，我认为在量子力学的世界里，最好去（从数学上）习惯——而不是去（从物理上）理解——所有东西。这也是我不很喜欢这门科学的原因。

一个态是希尔伯特空间里的一个右矢。观测量是厄密算符，观测值是算符的谱，对应本征态。

$S_{z}\left|S_{z} ;+\right\rangle=\frac{\hbar}{2}\left|S_{z} ;+\right\rangle, \quad S_{z}\left|S_{z} ;-\right\rangle=-\frac{\hbar}{2}\left|S_{z} ;-\right\rangle$

定义左矢是右矢的对偶，可以与右矢做内积、外积。定义正交、归一、完备等概念（略）。我们规定

$\begin{array}{l}{(\langle\beta|) \cdot(X|\alpha\rangle)=(\langle\beta| X) \cdot(|\alpha\rangle)} \\ {\text { bra } \quad \text { ket } \quad \text { bra } \quad \text { ket }}\end{array}$

对所有厄密算符，其本征值是实数，其本征态相互正交。

现在我们再来考虑1/2自旋系统。$S_{z}=(h / 2)[(|+\rangle\langle+|)-(|-\rangle\langle-|) ]$，$S_{z}| \pm\rangle=\pm(\hbar / 2)| \pm\rangle$。在这个地方顺手提一下升降算符（这时它比较自然）$S_{+} \equiv \hbar|+\rangle\left\langle-\left|, \quad S_{-} \equiv \hbar\right|-\right\rangle\langle+|$。那么

$S_{z} \doteq \frac{h}{2}\left(\begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right), \quad S_{+} \doteq \hbar\left(\begin{array}{cc}{0} & {1} \\ {0} & {0}\end{array}\right), \quad S_{-} \doteq h\left(\begin{array}{cc}{0} & {0} \\ {1} & {0}\end{array}\right)$

系统处在一个叠加态$\left|\alpha\right>$，规定一次测量得到某本征态的概率为$\text{prob for } a^{\prime}=\left|\left\langle a^{\prime} | \alpha\right\rangle\right|^{2}$。我们从实验知道了$\left|\left\langle+| S_{x} ;+\right\rangle\right|=\left|\left\langle-| S_{x} ;+\right\rangle\right|=\frac{1}{\sqrt{2}}$，因此$\left|S_{x} ;+\right\rangle=\frac{1}{\sqrt{2}}|+\rangle+\frac{1}{\sqrt{2}} e^{i \delta_{1}}|-\rangle$。同理$\left|S_{y} ; \pm\right\rangle=\frac{1}{\sqrt{2}}|+\rangle \pm \frac{1}{\sqrt{2}} e^{i \delta_{2}}|-\rangle$，$\delta_{2}-\delta_{1}=\pm\pi / 2$。我们出于方便，选取$\delta_1=0$，出于右手系的缘故，选取$\delta_2=\pi/2$。该选择对应的三个方向的自旋正对应广泛使用的泡利矩阵的形式。注意到几个事情：

$S_{ \pm}=S_{x} \pm i S_{y}$

$\left[S_{i}, S_{j}\right]=i \varepsilon_{i j k} \hbar S_{k}$

$\left[\mathbf{S}^{2}, S_{i}\right]=0$

两个观测量的泊松括号取零，说明它们compatible。这词的意思是说对一个量的测量行为不会对另一个量造成影响（显然，不同方向的自旋不compatible）。这词同时意味着这两个量的算符具有同一组基。利用这件事，我们可以把这组基记为collective index $K'$。很多时候，某个量的某个本征值对应不止一个态，区分它们就得靠另一个compatible的量的本征值。

不compatible的量的测量行为，例如自旋，是很奇特的。上图里（a）情况是加入测量仪器B，但每次都放出不同的$\left|b'\right>$再取平均，那么在最初滤过来$\left|a'\right>$的情况下，在最右边测量到$\left|c'\right>$的概率为$\left.\sum_{b^{\prime}}\left|\left\langle c^{\prime} | b^{\prime}\right\rangle\right|^{2}\left\langle b^{\prime} | a^{\prime}\right\rangle\right|^{2}=\sum_{b^{\prime}}\left\langle c^{\prime} | b^{\prime}\right\rangle\left\langle b^{\prime} | a^{\prime}\right\rangle\left\langle a^{\prime} | b^{\prime}\right\rangle\left\langle b^{\prime} | c^{\prime}\right\rangle$。但在（b）中没有测量仪器B，该概率为（式中加入了一个值为1 的因子）$\left|\sum_{b^{\prime}}\left\langle c^{\prime} | b^{\prime}\right\rangle\left\langle b^{\prime} | a^{\prime}\right\rangle\right|^{2}=\sum_{b^{\prime}} \sum_{b^{\prime \prime}}\left\langle c^{\prime} | b^{\prime}\right\rangle\left\langle b^{\prime} | a^{\prime}\right\rangle\left\langle a^{\prime} | b^{\prime \prime}\right\rangle\left\langle b^{\prime \prime} | c^{\prime}\right\rangle$。

要想它们相等，非得B和A或C compatible才行。对于不对易的物理量，测量似乎提供了，或者说产生了一个时间箭头的作用。

海森堡有一个不确定性原理。我们知道，A的dispersion为$\left\langle(\Delta A)^{2}\right\rangle=\left\langle\left(A^{2}-2 A\langle A\rangle+\langle A\rangle^{2}\right)\right\rangle=\left\langle A^{2}\right\rangle-\langle A\rangle^{2}$。对两个不同量来说，$\left\langle(\Delta A)^{2}\right\rangle\left\langle(\Delta B)^{2}\right\rangle \geq\left|\langle\Delta A \Delta B \rangle\right|^{2}$（schwarz不等式），而

$\begin{array}{c}{\langle\Delta A \Delta B\rangle=\frac{1}{2}\langle[A, B]\rangle+\frac{1}{2}\langle\{\Delta A, \Delta B\}\rangle} \\ {\text { . imaginary real}}\end{array}$

因此

$|\langle\Delta A \Delta B\rangle|^{2}=\frac{1}{4}|\langle[A, B]\rangle|^{2}+\frac{1}{4}|\langle\{\Delta A, \Delta B\}\rangle|^{2}$

可知

$\left\langle(\Delta A)^{2}\right\rangle\left\langle(\Delta B)^{2}\right\rangle \geq \frac{1}{4}|\langle[A, B]\rangle|^{2}$。

位置是一个可观测量，所以它也是一个算符。所以我们就说$x\left|x^{\prime}\right\rangle= x^{\prime}\left|x^{\prime}\right\rangle$。到了三维，$x\left|\mathbf{x}^{\prime}\right\rangle= x^{\prime}\left|\mathbf{x}^{\prime}\right\rangle, \quad y\left|\mathbf{x}^{\prime}\right\rangle= y^{\prime}\left|\mathbf{x}^{\prime}\right\rangle, \quad z\left|\mathbf{x}^{\prime}\right\rangle= z^{\prime}\left|\mathbf{x}^{\prime}\right\rangle$。根据我们的经验，任意两个方向的位置坐标都得compatible。即$\left[x_{i}, x_{j}\right]=0$。

从经典力学我们知道动量是位置的生成元。考虑一个无穷小位移变换，$\mathscr{T}\left(d \mathbf{x}^{\prime}\right)\left|\mathbf{x}^{\prime}\right\rangle=\left|\mathbf{x}^{\prime}+d \mathbf{x}^{\prime}\right\rangle$，它必须具备诸多性质，例如酉性，叠加性等，而满足这些性质的变换正是$\mathscr{T}\left(d \mathbf{x}^{\prime}\right)=1-i \mathbf{K} \cdot d \mathbf{x}^{\prime}$，$\mathbf{K}$的分量都是厄密算符。这里的生成元$\mathbf{K}$和动量差一个单位$\hbar$。这是规定单位制的时候造成的历史遗留问题。

由于$\left[\mathbf{x}, \mathscr{T}\left(d \mathbf{x}^{\prime}\right)\right]\left|\mathbf{x}^{\prime}\right\rangle= d \mathbf{x}^{\prime}\left|\mathbf{x}^{\prime}+d \mathbf{x}^{\prime}\right\rangle$，展开到一阶为$d \mathbf{x}^{\prime} |\mathbf{x}^{\prime} \rangle$，我们就有了$-i \mathbf{x K} \cdot d \mathbf{x}^{\prime}+i \mathbf{K} \cdot d \mathbf{x}^{\prime} \mathbf{x}=d \mathbf{x}^{\prime}$。把式子右边$d \mathbf{x}^{\prime}$的三个分量和左边对应起来，即可得$\left[x_{i}, K_{j}\right]=i \delta_{i j}$。从这一个式子结合上一节就可以得到我们中学时候了解的海森堡不确定性原理$\left\langle(\Delta x)^{2}\right\rangle\left\langle\left(\Delta p_{x}\right)^{2}\right\rangle \geq \hbar^{2} / 4$。

考虑非无穷小的位移变换，$\mathscr{T}\left(\Delta x^{\prime} \hat{\mathbf{x}}\right)=\lim _{N \rightarrow \infty}\left(1-\frac{i p_{x} \Delta x^{\prime}}{N \hbar}\right)^{N}=\exp \left(-\frac{i p_{x} \Delta x^{\prime}}{\hbar}\right)$。任意两个方向的位移变换都得compatible，对应动量也compatible。这样我们就有了三个"canonical commutation relations"（这个“正则”，怕是和“正则系综”没关系，而和“正则变换”有关系？）：

$\left[x_{i}, x_{j}\right]=0, \quad\left[p_{i}, p_{j}\right]=0, \quad\left[x_{i}, p_{j}\right]=i \hbar \delta_{i j}$

这和经典力学里的相关内容一一对应。

一般所说的（位置）波函数是某个态在位置基底上的各个投影。它的模的平方是概率密度，所以它的单位应该是$[V]^{-1/2}$。位置是个有连续谱的算符，动量也是，所以说这里的数学很乱，但是大多数地方只需要做两件事就可以推广之前对于分立谱的做法：把求和换成求积分；把 kronecker delta 换成 dirac delta。

位置波函数$\left\langle x^{\prime} | \alpha\right\rangle=\psi_{\alpha}\left(x^{\prime}\right)$。用它可以把各种东西都放到位置的基底下来考虑。比如说，$\langle\beta | \alpha\rangle=\int d x^{\prime} \psi_{\beta}^{*}\left(x^{\prime}\right) \psi_{\alpha}\left(x^{\prime}\right)$，$\langle\beta|f(x)| \alpha\rangle=\int d x^{\prime} \psi_{\beta}^{*}\left(x^{\prime}\right) f\left(x^{\prime}\right) \psi_{\alpha}\left(x^{\prime}\right)$。注意右边的f不是算符。我们也可以知道动量算符在位置基底下的写法：

$\begin{aligned}\left(1-\frac{i p \Delta x^{\prime}}{h}\right)|\alpha\rangle &=\int d x^{\prime} \mathscr{T}\left(\Delta x^{\prime}\right)\left|x^{\prime}\right\rangle\left\langle x^{\prime} | \alpha\right\rangle \\ &=\int d x^{\prime}\left|x^{\prime}+\Delta x^{\prime}\right\rangle\left\langle x^{\prime} | \alpha\right\rangle \\ &=\int d x^{\prime}\left|x^{\prime}\right\rangle\left\langle x^{\prime}-\Delta x^{\prime} | \alpha\right\rangle \\ &=\int d x^{\prime}\left|x^{\prime}\right\rangle\left\langle\left(x^{\prime}|\alpha\rangle-\Delta x^{\prime} \frac{\partial}{\partial x^{\prime}}\left\langle x^{\prime} | \alpha\right\rangle\right)\right.\end{aligned}$

从此可知$p|\alpha\rangle=\int d x^{\prime}\left|x^{\prime}\right\rangle\left(-i \hbar \frac{\partial}{\partial x^{\prime}}\left\langle x^{\prime} | \alpha\right\rangle\right)$。

同理，我们也可以写动量波函数$\left\langle p^{\prime} | \alpha\right\rangle=\phi_{\alpha}\left(p^{\prime}\right)$.我们将会发现，这两个波函数是一对傅里叶变换与逆变换。

容易知道$\left\langle x^{\prime}|p| \alpha\right\rangle=- i \hbar \frac{\partial}{\partial x^{\prime}}\left\langle x^{\prime} | \alpha\right\rangle$，故$\left\langle x^{\prime}|p| p^{\prime}\right\rangle=- i \hbar \frac{\partial}{\partial x^{\prime}}\left\langle x^{\prime} | p^{\prime}\right\rangle$，左边同时又是$-i \hbar \frac{\partial}{\partial x^{\prime}}\left\langle x^{\prime} | p^{\prime}\right\rangle$。因此（归一化之后）$\left\langle x^{\prime} | p^{\prime}\right\rangle=\frac{1}{\sqrt{2 \pi \hbar}} \exp \left(\frac{i p^{\prime} x^{\prime}}{h}\right)$，故

$\left\langle x^{\prime} | \alpha\right\rangle=\int d p^{\prime}\left\langle x^{\prime} | p^{\prime}\right\rangle\left\langle p^{\prime} | \alpha\right\rangle=\left[\frac{1}{\sqrt{2 \pi \hbar}}\right] \int d p^{\prime} \exp \left(\frac{i p^{\prime} x^{\prime}}{h}\right) \phi_{\alpha}\left(p^{\prime}\right)$

$\phi_{\alpha}\left(p^{\prime}\right)=\left[\frac{1}{\sqrt{2 \pi \hbar}}\right] \int d x^{\prime} \exp \left(\frac{-i p^{\prime} x^{\prime}}{\hbar}\right) \psi_{\alpha}\left(x^{\prime}\right)$

考虑一个高斯波包的例子。一个位置波函数$\left\langle x^{\prime} | \alpha\right\rangle=\left[\frac{1}{\pi^{1 / 4} \sqrt{d}}\right] \exp \left[i k x^{\prime}-\frac{x^{\prime 2}}{2 d^{2}}\right]$对应的$\langle x\rangle=0,\langle x^2\rangle=d^2/2,\langle p\rangle=\hbar k,\langle p^2\rangle=\hbar^2/2d^2+\hbar^2k^2$。可以看到，这个波包也满足海森堡不确定性原理。

第二章 量子动力学

现在通向万有理论的两条路中，最大的不可调和之一就是时空的问题：在量子力学当中，时间不是一个可观测量，而只是一个参数。在相对论性量子力学中，人们只是通过把位置x也降级成一个参数的形式来实现调和，而非把时间变为算符。因此，在我们的整个叙述当中，都需要注意：时间和空间是不平等的。

定义时间的演化$\left|\alpha, t_{0} ; t\right\rangle=\mathscr{U}\left(t, t_{0}\right)\left|\alpha, t_{0}\right\rangle$。和之前处理$\mathscr{T}$时相似，直接写出$\mathscr{U}\left(t_{0}+d t, t_{0}\right)=1-i \Omega d t$，$\Omega$是厄密算符。同样与经典结果对比知道$\Omega=\frac{H}{\hbar}$，这里的因子也是$1/\hbar$，这是为了保持经典下的规律$\frac{d \mathbf{x}}{d t}=\frac{\mathbf{p}}{m}$。

可以写出含时演化的薛定谔方程$i \hbar \frac{\partial}{\partial t} \mathscr{U}\left(t, t_{0}\right)=H \mathscr{U}\left(t, t_{0}\right)$。当$H$与时间无关的时候，容易解出$\mathscr{U}\left(t, t_{0}\right)=\exp \left[\frac{-i H\left(t-t_{0}\right)}{h}\right]$。我们在以下内容中基本上就只考虑这种情况。其他情况可以由带松级数来刻画。

可以看出来能量本征态是不演化的，随着时间的推移，它只是变化振幅。同样，对一个可观测量取能量本征态下的期望，也是不变化的。所以我们管能量本征态叫定态。但是考虑一个能量本征态的叠加态$\left|\alpha, t_{0}=0\right\rangle=\sum_{a^{\prime}} c_{a^{\prime}}\left|a^{\prime}\right\rangle$，算符$B$在该态的期望演化为$\sum_{a^{\prime}} \sum_{a^{\prime \prime}} c_{a^{\prime \prime}}^{*} c_{a^{\prime \prime}}\left\langle a^{\prime}|B| a^{\prime \prime}\right\rangle \exp \left[\frac{-i\left(E_{a^{\prime \prime}}-E_{a^{\prime}}\right) t}{h}\right]$，不同本征态对应的振动频率不一样。

考虑一个简单的例子。在自旋系统中取z方向的均匀磁场，$\omega \equiv \frac{|e| B}{m_{e} c}$，$H=\omega S_{z}$，$\mathscr{U}(t, 0)=\exp \left(\frac{-i \omega S_{z} t}{\hbar}\right)$。容易看出来，$\left|\alpha, t_{0}=0 ; t\right\rangle= c_{+} \exp \left(\frac{-i \omega t}{2}\right)|+\rangle+ c_{-} \exp \left(\frac{+i \omega t}{2}\right)|-\rangle$。如果初态取一个z方向的态，那么过多久还是同一个态。但是如果初态取一个x方向的态，例如$c_+=\pm c_-=\pm1/\sqrt{2}$，那么

$\left|\left\langle S_{x} \pm | \alpha, t_{0}=0 ; t\right\rangle\right|^{2}=\left\{\begin{array}{ll}{\cos ^{2} \frac{\omega t}{2},} & {\text { for } S_{x}+} \\ {\sin ^{2} \frac{\omega t}{2},} & {\text { for } S_{x}-}\end{array}\right.$

这个东西的物理意义类似于进动，实际上我们直接叫它自旋的进动。

时间和能量也有一种不确定性关系，但是必须强调：这和海森堡不确定性关系完全是本质不同的。这里面也没有任何泊松括号。

考虑两个态之间的关联振幅

$\begin{aligned} C(t) &=\left(\sum_{a^{\prime}} c_{a^{\prime}}^{*}\left\langle a^{\prime}\right|\right)\left[\sum_{a^{\prime \prime}} c_{a^{\prime \prime}} \exp \left(\frac{-i E_{a^{\prime \prime}} t}{\hbar}\right)\left|a^{\prime \prime}\right\rangle\right] \\ &=\sum_{a^{\prime}}\left|c_{a^{\prime}}\right|^{2} \exp \left(\frac{-i E_{a^{\prime}} t}{\hbar}\right) \end{aligned}$

我们假设能量连续分布，改写其为$C(t)=\int d E|g(E)|^{2} \rho(E) \exp \left(\frac{-i E t}{\hbar}\right)$。若它在$E_0$处取到一个峰，我们把$C(t)$写为

$C(t)=\exp \left(\frac{-i E_{0} t}{h}\right) \int d E|g(E)|^{2} \rho(E) \exp \left[\frac{-i\left(E-E_{0}\right) t}{h}\right]$

这个积分里的大部分都相互抵消，只有$|E-E_0|\simeq\hbar/t$ 的时候才不抵消。如果这个值比峰的宽度$\Delta E$小太多，还是没有用，还是会抵消掉。

因此有不确定性关系$\Delta t \Delta E \simeq \hbar$。

有两种常用的绘景：薛定谔和海森堡绘景。它们的区别在于分别把态和算符中的一个看做是含时演化的，另外一个则不动。不过，这只是数学/语法上的偏好，并不怎么影响物理。

要注意在海森堡绘景里面，如果写$H^{H}=\mathscr{U}^{\dagger} H^{S} \mathscr{U}$，那么对于“定态”有$|a^{H}\rangle=\mathscr{U}^\dagger|a^{S}\rangle$。

在海森堡绘景下，可以得出运动方程$\frac{d A^{(H)}}{d t}=\frac{1}{i \hbar}\left[A^{(H)}, H\right]$（注意，海森堡和哈密顿的首字母一样，可能造成混淆），与经典结果是一样的（除了泊松括号上的区别）。

可以证明，$\begin{array}{c}{\left[x_{i}, F(\mathbf{p})\right]=i \hbar \frac{\partial F}{\partial p_{i}}} \\ {\left[p_{i}, G(\mathbf{x})\right]=-i \hbar \frac{\partial G}{\partial x_{i}}}\end{array}$。我们接下来考虑这样一种情况：势阱中的粒子。$H=\frac{\mathbf{p}^{2}}{2 m}+V(\mathbf{x})$。这时，由运动方程，可以知道$\frac{d p_{i}}{d t}=\frac{1}{i \hbar}\left[p_{i}, V(\mathbf{x})\right]=-\frac{\partial}{\partial x_{i}} V(\mathbf{x})$。回想起$dx_i/dt=p_i/m$，代入之，即可得到$m \frac{d^{2} \mathbf{x}}{d t^{2}}=-\nabla V(\mathbf{x})$，或写为埃仑菲斯特定理$m \frac{d^{2}}{d t^{2}}\langle\mathbf{x}\rangle=\frac{d\langle\mathbf{p}\rangle}{d t}=-\langle\nabla V(\mathbf{x})\rangle$。实际上，它只是给了我们一种牛顿第二定律在量子世界尚未失去它的权柄的慰藉。

下面几节主要是介绍一些普遍的分析方法。它们代表着量子力学的三条进路：海森堡，薛定谔，费曼。

• 升降算符

升降算符是这门学科里的极其重要的工具，但以我目前的水平只能把它当做是一门技巧。我上量子力学这门课的时候，老师比较偏好于薛定谔方程，对这里近乎一笔带过。以至于即使我知道升降算符的广泛用处，却只会用它解一个问题。这问题就是$H=\frac{p^{2}}{2 m}+\frac{m \omega^{2} x^{2}}{2}$为哈密顿量的谐振子。

定义$a=\sqrt{\frac{m \omega}{2 \hbar}}\left(x+\frac{i p}{m \omega}\right), \quad a^{\dagger}=\sqrt{\frac{m \omega}{2 \hbar}}\left(x-\frac{i p}{m \omega}\right)$，分别是降、升算符。可以看出$\left[a, a^{\dagger}\right]=\left(\frac{1}{2 \hbar}\right)(-i[x, p]+i[p, x])=1$和$N=a^{\dagger} a$两个性质。此外，注意到$[N, a]=-a$，$\left[N, a^{\dagger}\right]=a^{\dagger}$。记$N|n\rangle= n|n\rangle$，那么$H|n\rangle=\left(n+\frac{1}{2}\right) \hbar \omega|n\rangle$。注意这地方我们已经（没费什么力气地）得到了H的本征态。可见：

$\begin{aligned} N a^{\dagger}|n\rangle &=\left(\left[N, a^{\dagger}\right]+a^{\dagger} N\right)|n\rangle \\ &=(n+1) a^{\dagger}|n\rangle \\ N a|n\rangle &=([N, a]+a N)|n\rangle \\ &=(n-1) a|n\rangle \end{aligned}$

这意味着$a|n\rangle= c|n-1\rangle$，a可以把能量降一个级，所以叫降算符。同理$a^\dagger$。算一下归一化，知道

$a|n\rangle=\sqrt{n}|n-1\rangle,a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle$

于是

$\begin{aligned}|1\rangle &= a^{\dagger}|0\rangle \\|2\rangle &=\left(\frac{a^{\dagger}}{\sqrt{2}}\right)|1\rangle=\left[\frac{\left(a^{\dagger}\right)^{2}}{\sqrt{2}}\right]|0\rangle \\|3\rangle &=\left(\frac{a^{\dagger}}{\sqrt{3}}\right)|2\rangle=\left[\frac{\left(a^{\dagger}\right)^{3}}{\sqrt{3 !}}\right]|0\rangle \\ & \vdots \\|n\rangle &=\left[\frac{\left(a^{\dagger}\right)^{n}}{\sqrt{n !}}\right] |0 \rangle \end{aligned}$

现在，知道$a|0\rangle= 0$，就知道$\left\langle x^{\prime}|a| 0\right\rangle=\sqrt{\frac{m \omega}{2 h}}\left\langle x^{\prime}\left|\left(x+\frac{i p}{m \omega}\right)\right| 0\right\rangle= 0$。它是一个关于波函数的方程：$\left(x^{\prime}+x_{0}^{2} \frac{d}{d x^{\prime}}\right)\left\langle x^{\prime} | 0\right\rangle= 0$。可以解出来这波函数是$\left\langle x^{\prime} | 0\right\rangle=\left(\frac{1}{\pi^{1 / 4} \sqrt{x_{0}}}\right) \exp \left[-\frac{1}{2}\left(\frac{x^{\prime}}{x_{0}}\right)^{2}\right]$。以此类推，解出每一级的波函数

$\left\langle x^{\prime} | n\right\rangle=\left(\frac{1}{\pi^{1 / 4} \sqrt{2^{n} n !}}\right)\left(\frac{1}{x_{0}^{n+1 / 2}}\right)\left(x^{\prime}-x_{0}^{2} \frac{d}{d x^{\prime}}\right)^{n} \exp \left[-\frac{1}{2}\left(\frac{x^{\prime}}{x_{0}}\right)^{2}\right]$

另外，使用

$\left\langle n^{\prime}|a| n\right\rangle=\sqrt{n} \delta_{n^{\prime}, n-1}, \quad\left\langle n^{\prime}\left|a^{\dagger}\right| n\right\rangle=\sqrt{n+1} \delta_{n^{\prime}, n+1}$

以及

$x=\sqrt{\frac{\hbar}{2 m \omega}}\left(a+a^{\dagger}\right), \quad p=i \sqrt{\frac{m h \omega}{2}}\left(-a+a^{\dagger}\right)$

可以得到各种东西的期望值。

考虑谐振子的含时演化。$\frac{d a}{d t}=\sqrt{\frac{m \omega}{2 \hbar}}\left(\frac{p}{m}-i \omega x\right)=-i \omega a$，解出来$a(t)=a(0) \exp (-i \omega t)$。是故$x(t)+\frac{i p(t)}{m \omega}=x(0) \exp (-i \omega t)+i\left[\frac{p(0)}{m \omega}\right] \exp (-i \omega t)$，对比实部虚部，可以知道x和p的含时演化。

这个地方的操作步骤是，首先把H除以一个能量子来无量纲化（算是马后炮），然后拆出升降算符，重新相乘得到H和$\hbar\omega aa^{\dagger}$之间的关系，写出升降的结果，确定下界$a|1\rangle=|0\rangle$，这时已经知道了能谱了；然后再递推各波函数，并用埃尔米特多项式表示；最后从升降算符的性质解含时演化。

对于初学者来说，升降算符是一个非常天马行空的主意。樱井似乎也没有给出一个相对自然的动机，只是表示“看到它的作用你们就知道这么构造的物理意义了”。我学的时候没学明白，现在在此揣测一下。首先把哈密顿量无量纲化，写成$H=\frac{x'^2+p'^2}{2}$，一方面，我们希望能找到一个算符$A$，使得它作用于H的一个本征态能够得到一个新的本征态。这个事情等价于$[H,A]\propto A$。同时我们又知道$dA/dt=[H,A]/i\hbar$。所以我们只需要找到一个量，其对时间的导数正比于它自己乘以$i$。另一方面，人们可能会习惯性地把H分解为$((p'-ix')/\sqrt{2})((p'-ix')/\sqrt{2})^*$，进而留意到$((p'-ix')/\sqrt{2})$对时间的导数正是它自己乘以$i$。至于这样找出来的本征态是不是完备，大概有数学家保驾护航，我就懒得考虑了。

需要留意的是，能量本征态是“定态”，这些态是不振的，叠加态才“振”。实际上，降算符$a$的本征态才对应经典谐振子。这态被称为相干态。

• 薛定谔方程

在学习经典力学的时候，我曾经了解到薛定谔方程和波动力学的灵感来源是经典力学里的哈密顿-雅克比方程。该方程把光的波动行为和粒子的行为联系在了一起。

写下波函数$\psi\left(\mathbf{x}^{\prime}, t\right)=\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle$，取哈密顿量$H=\frac{\mathbf{p}^{2}}{2 m}+V(\mathbf{x})$，其中势能满足$\left\langle\mathbf{x}^{\prime \prime}|V(\mathbf{x})| \mathbf{x}^{\prime}\right\rangle= V\left(\mathbf{x}^{\prime}\right) \delta^{3}\left(\mathbf{x}^{\prime}-\mathbf{x}^{\prime \prime}\right)$。从含时演化的薛定谔方程知道$\left\langle\mathbf{x}^{\prime}\left|\frac{\mathbf{p}^{2}}{2 m}\right| \alpha, t_{0} ; t\right\rangle=-\left(\frac{\hbar^{2}}{2 m}\right) \nabla^{\prime 2}\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle$，代入该式即得薛定谔方程

$i \hbar \frac{\partial}{\partial t} \psi\left(\mathbf{x}^{\prime}, t\right)=-\left(\frac{\hbar^{2}}{2 m}\right) \nabla^{\prime 2} \psi\left(\mathbf{x}^{\prime}, t\right)+V\left(\mathbf{x}^{\prime}\right) \psi\left(\mathbf{x}^{\prime}, t\right)$

概率密度是$\rho=|\psi|^2$。连续性方程要求$\frac{\partial \rho}{\partial t}+\nabla \cdot \mathbf{j}=0$。容易算出流j为$\left(\frac{h}{m}\right) \operatorname{Im}\left(\psi^{*} \nabla \psi\right)$。它和动量联系紧密：$\int d^{3} x \mathbf{j}(\mathbf{x}, t)=\frac{\langle\mathbf{p}\rangle_{t}}{m}$。

我们把波函数换种写法：

$\psi(\mathbf{x}, t)=\sqrt{\rho(\mathbf{x}, t)} \exp \left[\frac{i S(\mathbf{x}, t)}{h}\right]$

我们暂时还不知道相位的物理意义。但是注意到$\psi^{*} \nabla \psi=\sqrt{\rho} \nabla(\sqrt{\rho})+\left(\frac{i}{h}\right) \rho \nabla S$，我们发现

$\mathbf{j}=\rho\nabla S/m$

我们可以把$\nabla S/m$理解成某种速度。如果我们把它换成v，连续性方程就完全具有流体力学里的形式了：$\frac{\partial \rho}{\partial t}+\nabla \cdot\left(\rho\mathbf{v}\right)=0$。

记住这个物理意义。我们重新把薛定谔方程按这个波函数的写法，变成

$\begin{array}{l}{-\left(\frac{h^{2}}{2 m}\right)} \\ {\quad \times\left[\nabla^{2} \sqrt{\rho}+\left(\frac{2 i}{\hbar}\right)(\nabla \sqrt{\rho}) \cdot(\nabla S)-\left(\frac{1}{\hbar^{2}}\right) \sqrt{\rho}|\nabla S|^{2}+\left(\frac{i}{h}\right) \sqrt{\rho} \nabla^{2} S\right]+\sqrt{\rho} V} \\ {\quad=i \hbar\left[\frac{\partial \sqrt{\rho}}{\partial t}+\left(\frac{i}{h}\right) \sqrt{\rho} \frac{\partial S}{\partial t}\right]}\end{array}$

认为普朗克常数是小量：$\hbar\ll1,\hbar\left|\nabla^{2} S\right| \ll|\nabla S|^{2}$，得到

$\frac{1}{2 m}|\nabla S(\mathbf{x}, t)|^{2}+V(\mathbf{x})+\frac{\partial S(\mathbf{x}, t)}{\partial t}=0$

这就是经典力学里的哈密顿-雅克比方程。原来，波函数的相位就是作用量。以后，我们还会在路径积分里碰见这件事——我甚至觉得，这件事就是路径积分的动机之一。当然，确认无误的是，这就是启发薛定谔创立波动力学的动机。德布罗意的物质波的想法和普朗克的量子化的想法让薛定谔在十九世纪力学的基础上向前走了一大步。从这个意义上说，量子力学比统计力学更配叫做“mechanics”。

考虑一个能量E的定态。这个时候，可以把作用量里面分出一个哈密顿特征函数$W(x)=S(x,t)+Et$。那么经典的动量是$\mathbf{p}_{\text { class }}=\nabla S=\nabla W$。注意这和平面波$e^{-i\mathbf{k}\cdot\mathbf{x}-i\omega t}$的联系。

解薛定谔方程的一个近似方法是半经典近似（WKB近似）。考虑定态下

$\begin{aligned} S(x, t) &=W(x)-E t \\ &=\pm \int^{x} d x^{\prime} \sqrt{2 m\left[E-V\left(x^{\prime}\right)\right]}-E t \end{aligned}$

这时候$\rho$得是个定值，根据$\frac{\partial \rho}{\partial t}+\frac{1}{m} \frac{\partial}{\partial x}\left(\rho \frac{\partial S}{\partial x}\right)=0$，必须得$\rho \frac{d W}{d x}=\pm \rho \sqrt{2 m[E-V(x)]}=\text { constant }$。因此得到解

$\begin{aligned} \psi(x, t) \simeq &\left\{\frac{\text { constant }}{[E-V(x)]^{1 / 4}}\right\} \\ & \times \exp \left[ \pm\left(\frac{i}{h}\right) \int^{x} d x^{\prime} \sqrt{2 m\left[E-V\left(x^{\prime}\right)\right]}-\frac{i E t}{h}\right] \end{aligned}$

常数用归一化来定。

注意：我们的近似要求$h\left|\frac{d^{2} W}{d x^{2}}\right| \ll\left|\frac{d W}{d x}\right|^{2}$，即

$(\lambda/4\pi)(|dV/dx|)\ll E-V(x)$

意思是，在物质波多个波长的范围内，势能得没啥变化。我们的解在$E<V$的部分应该相应的变为

$\psi(\mathbf{x}, t)=\left\{\frac{\text { constant }}{[V(x)-E]^{1 / 4}}\right\} \exp \left[ \pm\left(\frac{1}{h}\right) \int^{x} d x^{\prime} \sqrt{2 m\left[V\left(x^{\prime}\right)-E\right]}-\frac{i E t}{h}\right]$

在$V=E$的附近，有一套标准流程：在E=V的根附近对V做线性的近似；在这根处求更近似的薛定谔方程$\frac{d^{2} u_{E}}{d x^{2}}-\left(\frac{2 m}{\hbar^{2}}\right)\left(\frac{d V}{d x}\right)_{x=x_{0}}\left(x-x_{0}\right) u_{E}=0$的严格解（贝塞尔），取到某个特定的阶；用连续性条件确定这个解的一些参数。说实话，这部分我完全不懂。

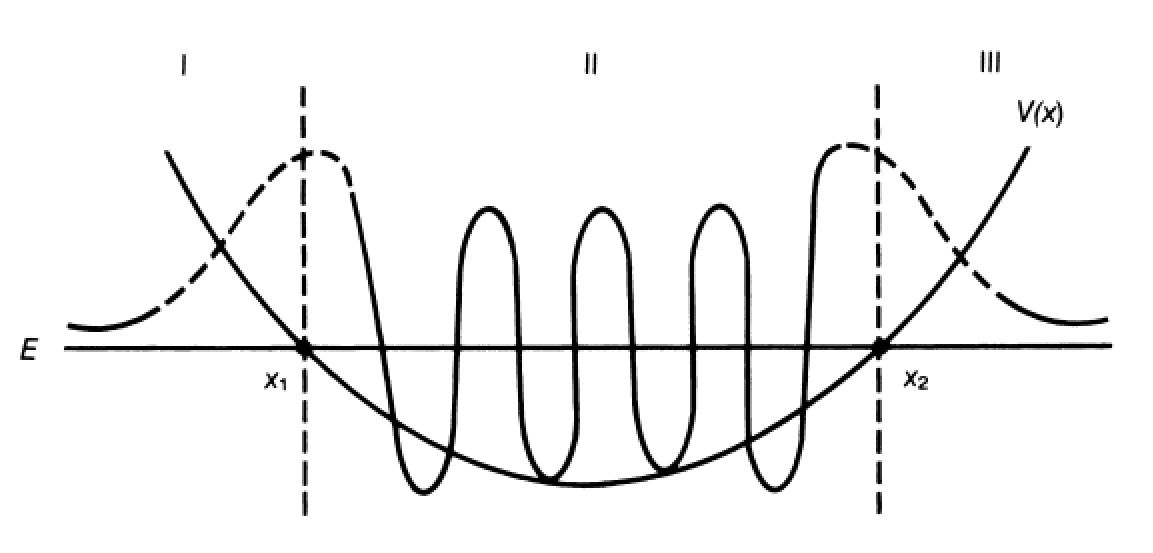
作者算了一个例子：自由落体的能级。

容易知道，在I区和III区都可以写$\left\{\frac{1}{[V(x)-E]^{1 / 4}}\right\} \exp \left[-\left(\frac{1}{h}\right) \int_{x}^{x_{1}} d x^{\prime} \sqrt{2 m\left[V\left(x^{\prime}\right)-E\right]}\right]$和$\left\{\frac{1}{[V(x)-E]^{1 / 4}}\right\} \exp \left[-\left(\frac{1}{h}\right) \int_{x_{2}}^{x} d x^{\prime} \sqrt{2 m\left[V\left(x^{\prime}\right)-E\right]}\right]$。从I区到II区，为了使解能够相容，把I区的解在复平面上绕过$x_1$延拓，这个过程由于分母里$(V-E)^{1/4}$的存在，会贡献一个$-\pi/4$的相位。从II到II，同理。这两个条件一约束，我们必须有分立的能级$\int_{x_{1}}^{x_{2}} d x \sqrt{2 m[E-V(x)]}=\left(n+\frac{1}{2}\right) \pi \hbar$（注意，左边实际上就是$\int pdq$，这个形式和索末菲的量子化$\oint p d q=n h$很像）。

这么个能级，据作者所说，能够在夸克偶素的研究中派上用场。

• 传播子和路径积分

取一个量子态，用能量本征态展开：

$\begin{aligned}\left|\alpha, t_{0} ; t\right\rangle &=\exp \left[\frac{-i H\left(t-t_{0}\right)}{h}\right]\left|\alpha, t_{0}\right\rangle \\ &=\sum_{a^{\prime}}\left|a^{\prime}\right\rangle\left\langle a^{\prime} | \alpha, t_{0}\right\rangle \exp \left[\frac{-i E_{a^{\prime}}\left(t-t_{0}\right)}{h}\right] \end{aligned}$

左乘一个位置的bra，得到$\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle=\sum_{a^{\prime}}\left\langle\mathbf{x}^{\prime} | a^{\prime}\right\rangle\left\langle a^{\prime} | \alpha, t_{0}\right\rangle \exp \left[\frac{-i E_{a^{\prime}}\left(t-t_{0}\right)}{h}\right]$。将它写成$\psi\left(\mathbf{x}^{\prime}, t\right)=\sum_{a^{\prime}} c_{a^{\prime}}\left(t_{0}\right) u_{a^{\prime}}\left(\mathbf{x}^{\prime}\right) \exp \left[\frac{-i E_{a^{\prime}}\left(t-t_{0}\right)}{h}\right]$，并注意到$c_{a^{\prime}}\left(t_{0}\right)=\int d^{3} x^{\prime} u_{a^{\prime}}^{*}\left(\mathbf{x}^{\prime}\right) \psi\left(\mathbf{x}^{\prime}, t_{0}\right)$，我们可以将新的波函数写成旧的波函数的积分变换的形式：

$\psi\left(\mathbf{x}^{\prime \prime}, t\right)=\int d^{3} x^{\prime} K\left(\mathbf{x}^{\prime \prime}, t ; \mathbf{x}^{\prime}, t_{0}\right) \psi\left(\mathbf{x}^{\prime}, t_{0}\right)$

其中

$K\left(\mathbf{x}^{\prime \prime}, t ; \mathbf{x}^{\prime}, t_{0}\right)=\sum_{a^{\prime}}\left\langle\mathbf{x}^{\prime \prime} | a^{\prime}\right\rangle\left\langle a^{\prime} | \mathbf{x}^{\prime}\right\rangle \exp \left[\frac{-i E_{a^{\prime}}\left(t-t_{0}\right)}{h}\right]$

就是传播子。实际上，从这个积分变换的形式可以看出来，传播子其实是薛定谔方程的格林函数，它正是方程

$\left[-\left(\frac{h^{2}}{2 m}\right) \nabla^{\prime \prime 2}+V\left(\mathbf{x}^{\prime \prime}\right)-i \hbar \frac{\partial}{\partial t}\right] K\left(\mathbf{x}^{\prime \prime}, t ; \mathbf{x}^{\prime}, t_{0}\right)=-i \hbar \delta^{3}\left(\mathbf{x}^{\prime \prime}-\mathbf{x}^{\prime}\right) \delta\left(t-t_{0}\right)$

在边界条件$K\left(\mathbf{x}^{\prime \prime}, t ; \mathbf{x}^{\prime}, t_{0}\right)=0, \quad t<t_{0}$之下的解。

举一个例子：考虑自由粒子，$H=p^2/2m$，其能量本征态也是动量本征态。考虑到$\langle x'|p'\rangle=e^{ip'x'/\hbar}$，我们可以解出传播子$K\left(x^{\prime \prime}, t ; x^{\prime}, t_{0}\right)=\left(\frac{1}{2 \pi \hbar}\right) \int_{-\infty}^{\infty} d p^{\prime} \exp \left[\frac{i p^{\prime}\left(x^{\prime \prime}-x^{\prime}\right)}{\hbar}-\frac{i p^{\prime 2}\left(t-t_{0}\right)}{2 m \hbar}\right]$。

易知该积分的结果是$K\left(x^{\prime \prime}, t ; x^{\prime}, t_{0}\right)=\sqrt{\frac{m}{2 \pi i h\left(t-t_{0}\right)}} \exp \left[\frac{i m\left(x^{\prime \prime}-x^{\prime}\right)^{2}}{2 \hbar\left(t-t_{0}\right)}\right]$。

传播子的一些性质值得考虑。

• 如果$t_0=0,$x’=x’’。这时候的传播子记为

  $\begin{aligned} G(t) & \equiv \int d^{3} x^{\prime} K\left(\mathbf{x}^{\prime}, t ; \mathbf{x}^{\prime}, 0\right) \\ &=\int d^{3} x^{\prime} \sum_{a^{\prime}}\left|\left\langle\mathbf{x}^{\prime} | a^{\prime}\right\rangle\right|^{2} \exp \left(\frac{-i E_{a^{t}} t}{h}\right) \\ &=\sum_{a^{\prime}} \exp \left(\frac{-i E_{a^{\prime}} t}{h}\right) \end{aligned}$

  具有与配分函数类似的形式。事实上，传播子（和路径积分）确实在统计力学里也发挥作用（我记得kardar讲了，可是一直没去看。。。）。

• 对上述$G(t)$做傅里叶-拉普拉斯变换：

  $\begin{aligned} \tilde{G}(E) & \equiv-i \int_{0}^{\infty} d t G(t) \exp (i E t / \hbar) / \hbar \\ &=-i \int_{0}^{\infty} d t \sum_{a^{\prime}} \exp \left(-i E_{a} t / \hbar\right) \exp (i E t / \hbar) / \hbar \end{aligned}$

  mathematica告诉我1）你需要回去复习复变积分，2）这玩意是$\tilde{G}(E)=\sum_{a^{\prime}} \frac{1}{E-E_{a^{\prime}}}$。所以说了解了$G$的奇点就了解了系统的能谱。

另外一方面，在海森堡的绘景下，传播子被表为

$\begin{aligned} K\left(\mathbf{x}^{\prime \prime}, t ; \mathbf{x}^{\prime}, t_{0}\right) &=\sum_{a^{\prime}}\left\langle\mathbf{x}^{\prime \prime} | a^{\prime}\right\rangle\left\langle a^{\prime} | \mathbf{x}^{\prime}\right\rangle \exp \left[\frac{-i E_{a^{\prime}}\left(t-t_{0}\right)}{h}\right] \\ &=\sum_{a^{\prime}}\left\langle\mathbf{x}^{\prime \prime}\left|\exp \left(\frac{-i H t}{\hbar}\right)\right| a^{\prime}\right\rangle\left\langle a^{\prime} |\operatorname{exp}\left(\frac{i H t_{0}}{\hbar}\right) | \mathbf{x}^{\prime}\right\rangle \\ &=\left\langle\mathbf{x}^{\prime \prime}, t | \mathbf{x}^{\prime}, t_{0}\right\rangle \end{aligned}$

在这个写法下，我们会发现

$\begin{aligned}\left\langle x_{N}, t_{N} | x_{1}, t_{1}\right\rangle=& \int d x_{N-1} \int d x_{N-2} \cdots \int d x_{2}\left\langle x_{N}, t_{N} | x_{N-1}, t_{N-1}\right\rangle \\ & \times\left\langle x_{N-1}, t_{N-1} | x_{N-2}, t_{N-2}\right\rangle \cdots\left\langle x_{2}, t_{2} | x_{1}, t_{1}\right\rangle \end{aligned}$

传说，费曼在读狄拉克的书的时候，注意到一个表述：

“$\exp \left[i \int_{t_{1}}^{t_{2}} \frac{d t L_{\text { classical }}(x, \dot{x})}{\hbar}\right]$ corresponds to $\left\langle x_{2}, t_{2} | x_{1}, t_{1}\right\rangle$”

他开始思考这个correspondence具体代表着什么。然后他就发明了路径积分。可以看到，这个指数项就是$e^{iS/\hbar}$也就是波函数的相位（的变化）。费曼记$S(n, n-1) \equiv \int_{t_{n-1}}^{t_{n}} d t L_{\mathrm{classical}}(x, \dot{x})$，对空间中每一条可能的路线，都有

$\prod_{n=2}^{N} \exp \left[\frac{i S(n, n-1)}{h}\right]=\exp \left[\left(\frac{i}{h}\right) \sum_{n=2}^{N} S(n, n-1)\right]=\exp \left[\frac{i S(N, 1)}{h}\right]$

然后传播子是这个相位变化对所有路径的积分。可以看到，对于大多数情况，相位振动剧烈，积分抵消；但是在$\delta S=0$附近的路径，则不抵消。因此这直接导致了经典理论中的最小作用量原理。

考虑一个势能$V(x)$。其具有

$\begin{aligned} S(n, n-1) &=\int_{t_{n-1}}^{t_{n}} d t\left[\frac{m \dot{x}^{2}}{2}-V(x)\right] \\ &=\Delta t\left\{\left(\frac{m}{2}\right)\left[\frac{\left(x_{n}-x_{n-1}\right)}{\Delta t}\right]^{2}-V\left(\frac{\left(x_{n}+x_{n-1}\right)}{2}\right)\right\} \end{aligned}$

其传播子的微元$\left\langle x_{n}, t_{n} | x_{n-1}, t_{n-1}\right\rangle=\left[\frac{1}{w(\Delta t)}\right] \exp \left[\frac{i m\left(x_{n}-x_{n-1}\right)^{2}}{2 \hbar \Delta t}\right]$。由于$\Delta\to0$的时候这东西趋于对$\Delta x$的$\delta$函数，可以算出$\frac{1}{w(\Delta t)}=\sqrt{\frac{m}{2 \pi i \hbar \Delta t}}$。这样，我们就可以定义一个算子

$\int_{x_{1}}^{x_{N}} \mathscr{D}[x(t)] \equiv \lim _{N \rightarrow \infty}\left(\frac{m}{2 \pi i \hbar \Delta t}\right)^{(N-1) / 2} \int d x_{N-1} \int d x_{N-2} \cdots \int d x_{2}$

并写出

$\left\langle x_{N}, t_{N} | x_{1}, t_{1}\right\rangle=\int_{x_{1}}^{x_{N}} \mathscr{D}[x(t)] \exp \left[i \int_{t_{1}}^{t_{N}} d t \frac{L_{\text { classical }}(x, \dot{x})}{h}\right]$

这就是费曼的路径积分。

我们来考虑规范变换下的量子力学。

• 首先，考虑一个势能零点的变化$$\tilde{V}(\mathbf{x})=V(\mathbf{x})+V_{0}$$。这个时候对于波函数的影响是$$\begin{aligned} \widehat{\left|\alpha, t_{0} ; t\right\rangle} &=\exp \left[-i\left(\frac{\mathbf{p}^{2}}{2 m}+V(x)+V_{0}\right) \frac{\left(t-t_{0}\right)}{\hbar}\right]|\boldsymbol{\alpha}\rangle \ &=\exp \left[\frac{-i V_{0}\left(t-t_{0}\right)}{\hbar}\right]\left|\boldsymbol{\alpha}, t_{0} ; t\right\rangle \end{aligned}$$

  这个影响仅涉及到相位。从它的形式上来看，经典效应（通过最小作用量原理）不能够展现这个变化的效果。但是考虑如下例子：一束粒子分两束，其一走高处，其二走低处，最终汇合时将产生干涉。这实验早已经做成了，它体现出重力的量子效应。特别的，由于相位差里面包括有质量，这告诉我们：在量子力学尺度上，重力并非纯粹的几何效应。

• 接下来，考虑电磁场的规范变换。

  • 在此之前，先把电磁场量子化：有哈密顿量$H=\frac{1}{2 m}\left(\mathbf{p}-\frac{e \mathbf{A}}{c}\right)^{2}+e \phi$，注意A和p并不对易（p是整个系统的动量，矢势A是电磁场部分的动量），因此平方项要写成$p^{2}-\left(\frac{e}{c}\right)(\mathbf{p} \cdot \mathbf{A}+\mathbf{A} \cdot \mathbf{p})+\left(\frac{e}{c}\right)^{2} \mathbf{A}^{2}$。注意到$$\frac{d x_{t}}{d t}=\frac{\left[x_{i}, H\right]}{i \hbar}=\frac{\left(p_{t}-e A_{i} / c\right)}{m}$$，取系统中粒子的动量$\Pi \equiv m \frac{d \mathbf{x}}{d t}=\mathbf{p}-\frac{e \mathbf{A}}{c}$，验证可得$\left[\Pi_{i}, \Pi_{j}\right]=\left(\frac{i \hbar e}{c}\right) \varepsilon_{i j k} B_{k}$。把H写成

    $\left[\Pi_{i}, \Pi_{J}\right]=\left(\frac{i \hbar e}{c}\right) \varepsilon_{i j k} B_{k}$

    并定义量子版本的洛伦兹力

    $m \frac{d^{2} \mathbf{x}}{d t^{2}}=\frac{d \Pi}{d t}=[\Pi,H]/i\hbar=e\left[\mathbf{E}+\frac{1}{2 c}\left(\frac{d \mathbf{x}}{d t} \times \mathbf{B}-\mathbf{B} \times \frac{d \mathbf{x}}{d t}\right)\right]$

    薛定谔方程便成了

    $\frac{1}{2 m}\left[-i \hbar \nabla^{\prime}-\frac{e \mathbf{A}\left(\mathbf{x}^{\prime}\right)}{c}\right] \cdot\left[-i \hbar \nabla^{\prime}-\frac{e \mathbf{A}\left(\mathbf{x}^{\prime}\right)}{c}\right]\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle$
    $+ e \phi\left(\mathbf{x}^{\prime}\right)\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle= i \hbar \frac{\partial}{\partial t}\left\langle\mathbf{x}^{\prime} | \alpha, t_{0} ; t\right\rangle$

    注意这个时候此方程对应的守恒流在变换$\nabla^{\prime} \rightarrow \nabla^{\prime}-\left(\frac{i e}{\hbar c}\right) \mathbf{A}$下成了$\mathbf{j}=\left(\frac{\hbar}{m}\right) \operatorname{Im}\left(\psi^{*} \nabla^{\prime} \psi\right)-\left(\frac{e}{m c}\right) \mathbf{A}|\psi|^{2}$。换种写法，$\mathbf{j}=\left(\frac{\rho}{m}\right)\left(\nabla S-\frac{e \mathbf{A}}{c}\right)$

  • 现在考虑规范变换$\phi \rightarrow \phi, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda$。（“规范变换”在电磁学里面指的是$\phi \rightarrow \phi-\frac{1}{c} \frac{\partial \Lambda}{\partial t}, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda$，但在本书中我们不考虑随时间变化的势能形式）令$\tilde{\mathbf{A}}=\mathbf{A}+\nabla \Lambda$，我们要求

    $\langle\alpha|\mathbf{x}| \alpha\rangle=\langle\tilde{\alpha}|\mathbf{x}| \tilde{\alpha}\rangle$
    $\left\langle\alpha\left|\left(\mathbf{p}-\frac{e \mathbf{A}}{c}\right)\right| \alpha\right\rangle=\left\langle\tilde{\alpha}\left|\left(\mathbf{p}-\frac{e \tilde{\mathbf{A}}}{c}\right)\right| \tilde{\alpha}\right\rangle$

    $\langle\alpha | \alpha\rangle=\langle\tilde{\alpha} | \tilde{\alpha}\rangle$

    前两式是因为粒子的轨迹是不受规范变换影响的。可以得到$|\tilde{\boldsymbol{\alpha}}\rangle=\mathscr{G}|\alpha\rangle$中的变换G满足$\mathscr{G}=\exp \left[\frac{i e \Lambda(\mathbf{x})}{\hbar c}\right]$.从波函数的形式可以推出来变换导致$S \rightarrow S+\frac{e \Lambda}{c}$，这正好使得流 j 是规范不变的。

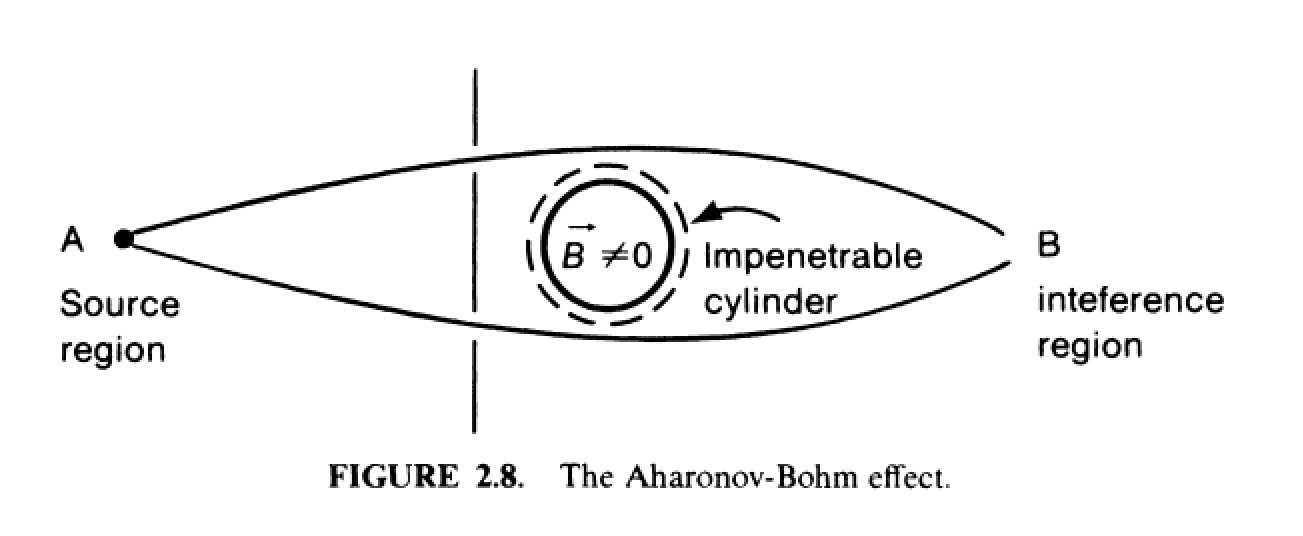
  • 阿哈罗诺夫-玻姆效应是一个很好的例子。它体现了矢势作为物理实体而非一种数学工具的效应。

    

    考虑这个情况。磁场（磁感线）被限制在圆柱壳里面（但圆柱外面有矢势，其值可以算得为$\mathbf{A}=\left(\frac{B \rho_{a}^{2}}{2 \rho}\right) \hat{\phi}$），而从圆柱上方和下方走的粒子将会受到矢势的影响。

    从电磁学的结果，可以知道对于电磁场中的粒子，其拉氏量多了一项$\frac{e}{c} \frac{d \mathbf{x}}{d t} \cdot \mathbf{A}$，其作用量多了一项$\frac{e}{c} \int_{t_{n-1}}^{t_{n}} d t\left(\frac{d \mathbf{x}}{d t}\right) \cdot \mathbf{A}$。在路径积分中，这带来的影响是$\Pi \exp \left[\frac{i S^{(0)}(n, n-1)}{\hbar}\right] \rightarrow\left\{\Pi \exp \left[\frac{i S^{(0)}(n, n-1)}{\hbar}\right]\right\} \exp \left(\frac{i e}{\hbar c} \int_{\mathbf{x}_{1}}^{\mathbf{x}_{N}} \mathbf{A} \cdot d \mathbf{s}\right)$

    因此，从上面走的粒子的相位变化是$\left\{\exp \left[\left(\frac{i e}{\hbar c}\right) \int_{\mathbf{x}_{1}}^{\mathbf{x}_{N}} \mathbf{A} \cdot d \mathbf{s}\right]_{\text { above }}\right\}$，从下面走的粒子的相位变化是$\left\{\exp \left[\left(\frac{i e}{\hbar c}\right) \int_{\mathbf{x}_{1}}^{\mathbf{x}_{N}} \mathbf{A} \cdot d \mathbf{s}\right]_{\text { below }}\right\}$。发生干涉地点的相位差，即二者之差恰好是

    $\left[\left(\frac{e}{\hbar c}\right) \int_{\mathbf{x}_{1}}^{\mathbf{x}_{N}} \mathbf{A} \cdot d \mathbf{s}\right]_{\text { above }}-\left[\left(\frac{e}{\hbar c}\right) \int_{\mathbf{x}_{1}}^{\mathbf{x}_{N}} \mathbf{A} \cdot d \mathbf{s}\right]_{\text { below }}=\left(\frac{e}{\hbar c}\right) \oint \mathbf{A} \cdot d \mathbf{s}$

    正比于圆柱体内的磁通量。从这个意义上来说，矢势是比磁感应强度更基本的物理量。

在这边谈起规范变换，好像总是一个波函数相位的变换，但是所谓规范的gauge，实际上是从德语Eich来的，意为度量。考虑函数$F(x)$，其在某点处展开为$F(x+dx)=F(x)+(\nabla F(x))dx$。现在做“规范”变换，让$1|_x=(1+\Sigma(x)dx)|_{x+dx}$，那么$F(x+dx)=F(x)+[(\nabla+\Sigma)F]|_xdx$。这里和因子$\mathscr{G}=\exp \left[\frac{i e \Lambda(\mathbf{x})}{\hbar c}\right]$对比的就是$e^{\Sigma}$。这才是规范变换原本的含义。现在虽然意义不完全一样了，但是规范变换的名字还是留着。

关于解薛定谔方程

出于实用的考虑，我来写一下一些作者认为比较简单的情形中关于薛定谔方程的相关事情。参考资料是朗道的卷3.

自由粒子的薛定谔方程

它的解是$\psi\propto e^{i/\hbar\cdot(\mathbf{p}\cdot\mathbf{r}-Et)}$，一个平面波。它正是该粒子的德布罗意物质波。

薛定谔方程中关于势能的基本性质

• 波函数在整个空间必须得是单值的，连续的。一般来讲，导数也是连续的。不过，V达到无穷大，则波函数必须取0，在界面上也是这样。在界面上的导数一般不连续。
• V不发散，或在某一点发散但不超过$-1/r^s,s<2$，则波函数也不发散。事实上，考虑原点附近一个有坐标不确定度$r_0$的波包，它相当于在$r_0$内取有限值，在外为0。那么其动量不确定度$\sim \hbar/r_0$，动能的不确定度或均值$\sim 1/r_0^2$，故总能量在$s<2$并不能成任意大的负值。
• 若V在无穷远消失，则其所有负能量态都是束缚态，离散谱。因为任何连续谱中的定态都对应于无限运动。
• 假定无穷远处势能为负并按$r^{-s}$趋于0.这个时候，如果$s<2$，则对于离原点足够远的情况，总有能量为负的情况开始出现，并最终收敛到0. 离散谱中有无穷多个能级，它们越来越密集地挤向0. 反之，离散谱的能级数目则是有限的。
• 对于s=2的情形需要在后面单独讨论。

一维运动的一般性质

考虑薛定谔方程$d_{xx}\psi+2m/\hbar^2(E-V)\psi=0$。

• 所有离散谱能级均无简并。
• 假定波函数在数轴两头收敛。为了方便，写$V(\infty)=0$，$V(-\infty)=V_0>0$。离散谱对应$V_{min}<E<0$。对于连续谱，在$E\in(0,V_0)$内，波函数在右侧显示出驻波$a\cos(kx+\delta)$，在左侧显示出指数衰减$be^{\kappa x}$。最后，在$V_0$以上，显示出两个方向的波$a_!e^{ikx}+a_2e^{-ikx}$。
• 如果想把波函数按着能量的$\delta$函数归一化，那么把其渐进表达式写成$A(e^{i(kx+\delta)}+e^{-i(kx+\delta)})$，然后让能运动到无穷远处的平面波（们）的概率流密度之和为$1/2\pi\hbar$以求出归一化系数。该流密度满足刘维尔方程$\partial_{t}|\psi|^2+\nabla\cdot j=0$。这个系数（$\propto1/\sqrt{2\pi\hbar v}$）的来源就是从x变到p的傅里叶变换的$2\pi$，从k到p的$\hbar$，以及从p到E的$\sqrt{v}$。

方势阱

• 对于有限深度的势阱，使用连续性条件$\psi'/\psi$连续可以简化计算。

透射系数

• 考虑一个相互作用的尺度a，势能$V(x)$在$|x|\gg a$时迅速减小。可以求$E\to0$时透射系数趋于零的规律。如下作：取从左边入射，在右边渐进式为$Ae^{ikx}$，左边渐进式为$e^{ikx}+Be^{-ikx}$，$k=\sqrt{2mE}/\hbar$。如果在$k|x|\ll1, |x|\gg a$的区域，能量和势能都可以略去，薛定谔方程的解在x为正或负时的$\psi=a_{1, 2}+b_{1, 2}x$。由中间的诸段$\psi$的形式可以从各种分界处条件得到$a_1=\rho a_2+\mu b_2,b_1=\nu a_2+\tau b_2$。这些希腊字母都是和能量无关的实数（因为薛定谔方程中已经没有能量了）。另一方面，渐进式的展开必须能够与这一次函数形式的波函数对齐，所以$a_1=1+B,b_1=ik(1-B),a_2=A,b_2=ikA$，在k较小时，可以解得$A\approx 2ik/\nu$，透射系数$D\propto k^2\propto E$。

  故它与能量成正比地趋于0。

有心力场

NOTE：这个地方本来应该是引入一点对称性和群论的最好的时机（樱井也是这么做的），但是我感到复（预）习的紧迫，而不得不暂时丧掉学习的热情，从一些别的课本里面（他们把对称性放在很后面来讲）来学这一段。

旋转的不变性产生了角动量的守恒量，假设旋转的无穷小变化有形式$1-iRd\phi$，$iR=r\times\nabla$，$\hbar l=r\times p =-i\hbar r\times\nabla$。这个量纲还是选择在p里面放一个hbar的结果。容易得到$[l_i, A_k]=i\epsilon_{ikl}A_l$，$[l^2, l_i]=0$。

一般来说角动量的问题都是用球坐标来算。在这个时候$z$轴下面的角动量的算符的表示特别好（$l_z=-i\partial_\phi$），这部分的本征函数就直接是$\Phi_m=\frac{1}{\sqrt{2\pi}}e^{im\phi},m\in\mathbb{Z}$。所以一般首先特别关心哪个方向的角动量就把它设成z轴。另外一方面，由于z轴可以随便取，量子数m只能取整数的要求看起来可能不合理，但是注意——两个方向上的角动量是不对易的，除非其同时为0。这样的不对易性质一般要求能级的简并：取$l_x$的一个本征态$\psi$，$l_y\psi$和$\psi$不是一个态，却有相同的本征值。

可以证明，在这种问题下$l_z$和$l^2$就构成一个compatible set。其中$l^2$可以证明是对应$\nabla_{\theta, \phi}/(-r^2)$，那个算符的意思是laplacian的角部。对于具有确定的总角动量的系统，肯定存在着一些简并的$\Phi_m$，这是从z轴的对称性得知的。人们在解这系统的时候使用与振子问题中相似的升降算符。我们把$l^2$拆开，写成$l^2=l_+l_-+l_z^2-l_z$，其中$l_\pm=l_x\pm l_y$。容易得到$[l_z,l_\pm]=\pm l_\pm$。知道这些信息之后，就针对性地得到$l_zl_\pm\psi_m=(m\pm1)l_\pm\psi_m$。在振子问题中，是找降不动的态来确定本征值的，现在我们看升不动的态（总角动量给定，$l^2-l_z^2$不能是负的，限制m的值）。$l_+\psi_l=0$，左乘一个$l_-$，可以算出$l(l+1)$，其中$l$是m能取的上限。

我们称一个系统的角动量为l，其含义为其总角动量的平方的本征值是l(l+1)。从$l^2,l_z$对角化的表象下计算$l_{x,y}$的矩阵元，可以先算$l_\pm$的矩阵元。容易知道：$l^2$，$l_z$都对角化了，$l_\pm$非零的矩阵元只有对角线上(下)相邻的一条。已知有

$l^2=l_+l_-+l_z^2-l_z$

两边取对角元

$l(l+1)=\langle m|l_+|m-1\rangle\langle m-1|l_-|m\rangle+m^2-m=|\langle m|l_+|m-1\rangle|^2+m^2-m$

因此$\langle m|l_+|m-1\rangle=\sqrt{(l+m)(l-m+1)}$。剩下的步骤都非常简单了。

不加证明，但可以理解地写出角动量的本征函数$Y_{lm}=\Theta_{lm}\Phi_m=(-)^{(m+|m|)/2}i^l\sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}(\cos\theta)e^{im\phi}$，其中$P$是连带勒让德多项式。

这节叫“有心力场”，所以先跳过选择定则和角动量相加之类的东西。我们来看径向波函数怎么算。首先，两个相互作用的粒子，其哈密顿量为$H=-\frac{\hbar^{2}}{2 m_{1}} \Delta_{1}-\frac{\hbar^{2}}{2 m_{2}} \Delta_{2}+U(r)$。用惯常的办法，分解成$H=-\frac{\hbar^{2}}{2\left(m_{1}+m_{2}\right)} \triangle_{R}-\frac{\hbar^{2}}{2 m} \triangle+U(r)$，m是约化质量。除去重心运动对应的自由粒子部分之外，薛定谔方程$\Delta \psi+\left(2 m / \hbar^{2}\right)[E-U(r)] \psi=0$，改写为球坐标下的

$\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2}{\frac{\partial \psi}{\partial r}}\right)+\frac{1}{r^{2}}\left[\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} \psi}{\partial \phi^{2}}\right]+\frac{2 m}{\hbar^{2}}[E-U(r)] \psi=0$

在式中带入$l^2$对应的东西，大大简化求解流程：$\frac{\hbar^{2}}{2 m}\left[-\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \psi}{\partial r}\right)+\frac{l^2}{r^{2}} \psi\right]+U(r) \psi=E \psi$

现在我们定着l和m来求解径向波函数，其满足$\psi=R(r)Y_{lm}(\theta,\phi)$。解这个东西的操作是做变换$R(r)=\chi(r) / r$然后得到

$\frac{\mathrm{d}^{2} \chi}{\mathrm{d} r^{2}}+\left[\frac{2 m}{\hbar^{2}}(E-U)-\frac{l(l+1)}{r^{2}}\right] \chi=0$

这相当于在方程里面加了一项离心能$\frac{l^2\hbar^2}{2mr^2}$。函数$\chi$的归一化由$\int_0^\infty|\chi|^2dr=1$确定。径向波函数的能谱用下标n表示。一般管nml分别叫径量子数，角量子数，磁量子数。

• 原点附近，如果满足$U(r)r^2\to0$，方程可以简化成$\mathrm{d}\left(r^{2} \mathrm{d} R / \mathrm{d} r\right) / \mathrm{d} r-l(l+1) R=0$，解出来$R\sim r^l$。

• 球面波。类比平面波的情形，$U=0$。略去解的过程，其径向波函数正比于球贝塞尔函数：

  $\begin{aligned} R_{k l}=& \sqrt{( 2 \pi k / r )} J_{l+1 / 2}(k r)=2 k j_{l}(k r) \\ j_{l}(x) &=\sqrt{(\pi/2 x )} J_{l+1 / 2}(x) \end{aligned}$

  该函数在远处的渐进行为是$\frac{2 \sin \left(k r-\frac{1}{2} l \pi\right)}{r}$。

• 现在考虑$U\sim -\beta/r^2$的特殊情况。在原点附近的行为满足$R^{\prime \prime}+2 R^{\prime} / r+\gamma R / r^{2}=0$，其中$\gamma=2 m \beta / \hbar^{2}-l(l+1)$。取$R\sim r^s$，可以解s的二次方程。若有两实根，则粒子不落入力心。反之，则落入力心。

• 考虑库仑势的情形：$\frac{\mathrm{d}^{2} R}{\mathrm{d} r^{2}}+\frac{2}{r} \frac{\mathrm{d} R}{\mathrm{d} r}-\frac{l(l+1)}{r^{2}} R+\frac{2 m}{\hbar^{2}}\left(E+\frac{\alpha}{r}\right) R=0$。这相当于解氢原子的波函数，薛定谔一开始就是做的这事。做法是这样的：

  • 按着库伦单位制把方程变掉：$\frac{\mathrm{d}^{2} R}{\mathrm{d} r^{2}}+\frac{2}{r} \frac{\mathrm{d} R}{\mathrm{d} r}-\frac{l(l+1)}{r^{2}} R+2\left(E+\frac{1}{r}\right) R=0$

  • 引入参量$n=1 / \sqrt{( -2 E )}, \quad \rho=2 r / n$，变成$R^{\prime \prime}+\frac{2}{\rho} R^{\prime}+\left[-\frac{1}{4}+\frac{n}{\rho}-\frac{l(l+1)}{\rho^{2}}\right] R=0$

  • 考虑在远处的渐进行为：$R''=R/4$。加上在原点附近已知的渐进行为，可以知道$R=\rho^{l} e^{-\rho / 2} w(\rho)$。

  • 方程$\rho w^{\prime \prime}+(2 l+2-\rho) w^{\prime}+(n-l-1) w=0$的解是合流超几何函数$w=F(-n+l+1,2 l+2, \rho)$，并且要求$-(-n+l+1)\in\mathbb{N}$。据此知道$l=0, \cdots, n-1$，总的简并度可以求出是$n^2$。（离散部分）能谱转换回SI单位制的话是$E=-m \alpha^{2} / 2 \hbar^{2} n^{2}$。

• （以下两小点需要了解更多的数学知识之后补充）可观测量的本征谱的简并对应着体系的某种对称性，这是一个可以严格描述和证明的事情。现在暂时就理解成简并对应着需要塞进来凑成compatible set的额外的守恒量好了。在这个例子中，额外的简并度（$n^2>2l+1$，后者是SO(3)的不可约表示维数）对应着$r^{-1}$势的一个额外的守恒量：LRL（拉龙楞）矢量。（实际上，朗道指出，通过LRL矢量和角动量的线性组合，我们可以凑出来两个三维物理量，它们满足两个独立的三维角动量矢量的对易关系。。LRL矢量的存在让这个问题更像SO(4)了，但是我觉得这个地方并没有SO(4)的物理意义。）

• 更进一步的，由贝特朗定理，只有径向谐振子和库仑势下的粒子，其轨道在微扰下闭合。也只有这两种有心力下会产生额外的对称性，进而导致额外的简并度。

微扰

同样，这部分也是出于预习的考虑。

现在只讨论与时间无关的微扰。考虑某一给定系统，具有哈密顿量$H=H_0+V$。$V$可以被看做微扰项的必要条件是$V_{mn}\ll|E_m-E_n|$，之后将证明这个结论。我们如果已知没有能级简并的精确解$H_0\psi^0_n=E^0_n \psi^0_n$，要求$H\psi_n=E_n\psi_n$的近似解，则首先把$\psi$展开为$\psi_n=\sum c_{nm}\psi^0_m$，代入，并左乘一个$\psi^0_k$，得到

$\left(E_n-E_{k}^{0}\right) c_{nk}=\sum V_{k m} c_{nm}$

把$E_n$和$c_{nm}$写成级数，此时可以令$c_{nm}=\delta_{nm}$。（kronecker delta）求第一级近似时，注意到V本身也是一个一阶小，得到$k=n$时$E_n^{(1)}=V_{nn}$，$k\neq n$时$c_{nk}^{(1)}=V_{kn}/(E_n^{(0)}-E_k^{(0)})$。在这里就可以看到那个必要条件的合理性。还差$c_{nn}^{(1)}$没有选取，由于$\psi_n^{(0)}+\psi_n^{(1)}$归一化的要求，这个量必须为0.

可以算出物理量f的微扰值。利用$\psi_{n}^{(1)}=\sum_{m}^{m\neq n} \frac{V_{m n}}{E_{n}^{(0)}-E_{m}^{(0)}} \psi_{m}^{(0)}$，可以得到$f_{n m}=f_{n m}^{(0)}+\sum_{k}^{k\neq n} \frac{V_{n k} f_{k m}^{(0)}}{E_{n}^{(0)}-E_{k}^{(0)}}+\sum_{k}^{k\neq m} \frac{V_{k m} f_{n k}^{(0)}}{E_{m}^{(0)}-E_{k}^{(0)}}$。

如果有简并，展开就要麻烦些：我们可以把一个能级下的所有本征函数写成它们的另一组任意的线性组合。但是，在微扰下保持改变很小的限制下，这个线性组合不再是任意的了。选取$\psi_{nl}^0$为第n个能级的第l个本征态，正确的第k个零级近似波函数应该是$\sum c_{k,ln}^{(0)}\psi_{nl}^{0}$。考虑最低阶近似，$V\sum c_{k,ln}^{(0)}\psi_{nl}^{(0)}=E_n^{(1)}\sum c_{k,ln}^{(0)}\psi_{nl}^{(0)}$，变为$E_n^{(1)}c_{k,l'n}^{(0)}=\sum V_{nl'l}c_{k,ln}^{(0)}$。于是

$\sum(V_{nl'l}-E_n^{(1)}\delta_{l'l})c_{k,l'n}^{(0)}=0$

我们先解它的系数行列式（让它为0以确保有非零解），解出能量一级修正，再带回去算出线性组合的系数c。我们注意到，简并被微扰所解除了。