ML笔记（5）

发表于 更新于 分类于 ， Waline： 本文字数： 17k 阅读时长 ≈ 15 分钟

week 9,10

气氛突然数学起来。

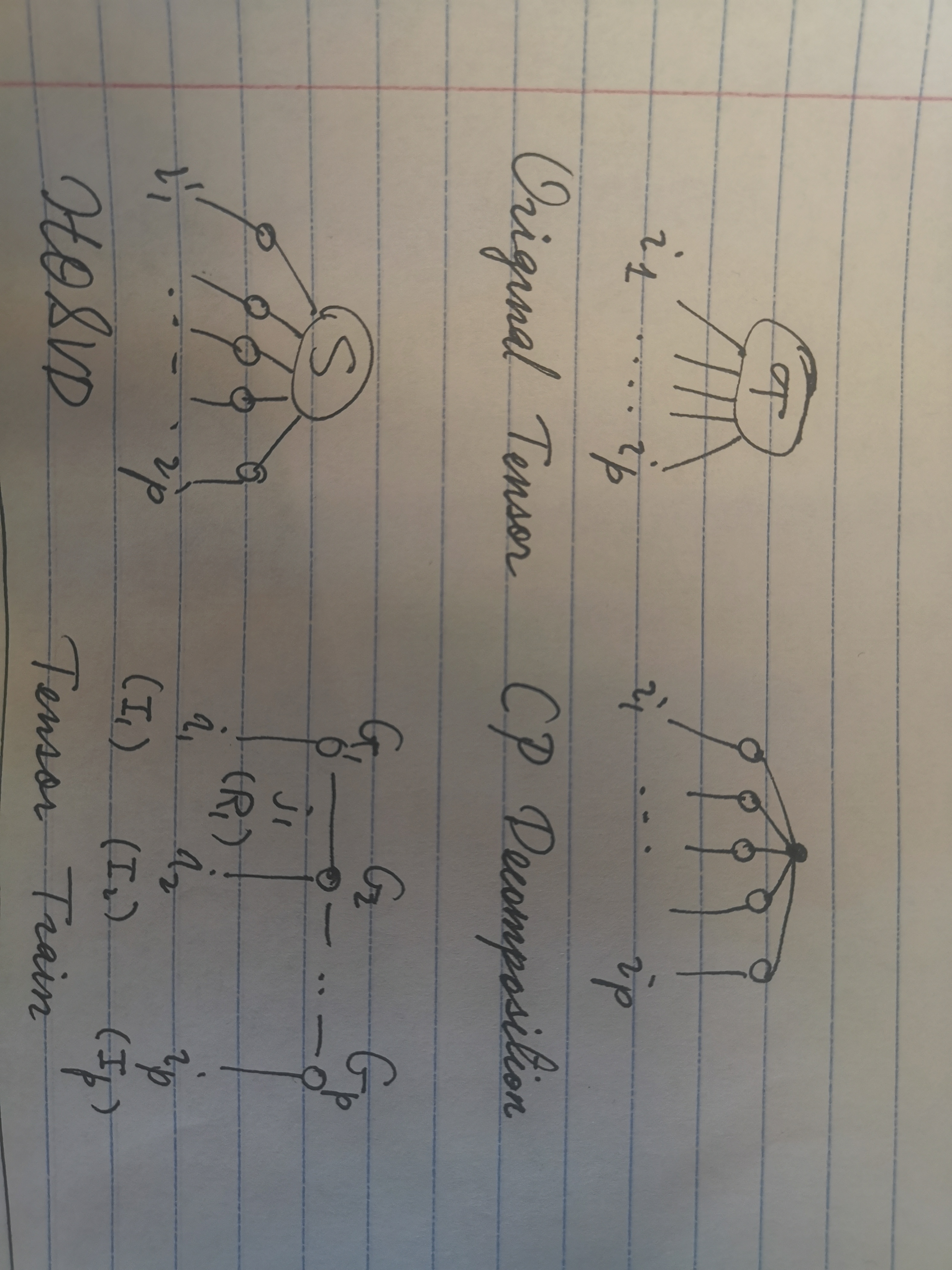
这次讲的基本上就是张量——张量积，张量的分解（CP-Decomposition， HOSVD）。之前我们处理矩阵，用的是SVD和eigenset的分解，动机是在低维上把握矩阵的行为，进而把握这些矩阵对应的高维数据集的性质。对于张量，很容易想到如法炮制。但是不幸的是，尽管矩阵的分解是一个相对容易的套路，张量的decomposition却是一个NP-hard的问题。

  • 何为张量

    有三种定义。

    • free vector space中的等价类。——QM里面，用的是这个定义。我们在这个讲义里用的也是这个定义。
    • basis变换时满足某种特定变换规则的对象。——GR里面我学到的就是这个。这也是我在课上唯一听懂的部分。
    • “linearizer of multilinear maps”——一个数学家可能会喜欢的说法。与本课的内容和我的兴趣都无关。

    对于我不幸的大脑来说，这些定义都太数学了。况且，我不像许多其他同学一样学过许多高明的量子场论。因此，在了解这些定义的具体内容之前，不妨先产生一个模糊的概念：张量是线性映射之间的线性映射。

  • 第一个定义的解释

    取n1,…,nkn_{1}, \dots, n_{k}维欧氏空间V1,…,VkV_{1}, \ldots, V_{k}，令F\mathcal{F}代表这些空间的cartesian积生成的所谓"free vector space"，这就是说，Cartesian积得到的∑ni\sum n_i维空间中的每一个元素都是该空间的一个basis（现在，忘掉直和空间中的线性性）。一开始，我还以为V1×V2×…×VkV_{1} \times V_{2} \times \ldots \times V_{k}就是F\mathcal{F}呢。实际上，Cartesian Product弄出来的这东西叫直和，维数是∑ni\sum n_i；直积得到的空间，维数是∏ni\prod n_i。

    令M\mathcal{M}是由形如

    (x1,…,xi−1,xi+yi,xi+1,…,xk)−(x1,…,xi−1,xi,xi+1,…,xk)−(x1,…,xi−1,yi,xi+1,…,xk)\left(x_{1}, \ldots, x_{i-1}, x_{i}+y_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, x_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, y_{i}, x_{i+1}, \ldots, x_{k}\right)

    和

    α(x1,…,xi−1,xi,xi+1,…,xk)−(x1,…,xi−1,αxi,xi+1,…,xk)\alpha\left(x_{1}, \ldots, x_{i-1}, x_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, \alpha x_{i}, x_{i+1}, \ldots, x_{k}\right)

    的元素构成的子空间。那么，直积V1⊗⋯⊗VkV_{1} \otimes \cdots \otimes V_{k}就是商空间F/M\mathcal{F} / \mathcal{M}。商空间的意思就是说，对于F\mathcal{F}中的元素F, f，F=f+m,m∈MF=f+m,m\in\mathcal{M}，那么这两个元素属于同一个等价类，这些等价类的集合就是商空间。一个简单的例子。取V1V_1，V2V_2。他们的基是{vk}\{v_k\}，{wk}\{w_k\}。V1×V2V_1\times V_2的基底是{(vi,0)+(0,wj)}\{(v_i,0)+(0,w_j)\}。V1⊗V2V_1\otimes V_2的基底是{(vi,wj)}\{(v_i, w_j)\}。

    为什么说这个定义是QM里面采用的呢？在QM里面，量子态的直积满足以下性质：

    ψ1⊗(ϕ1+ϕ2)=ψ1⊗ϕ1+ψ1⊗ϕ2;αψ⊗ϕ=ψ⊗(αϕ)=α(ψ⊗ϕ)\psi_1\otimes(\phi_1+\phi_2)=\psi_1\otimes\phi_1+\psi_1\otimes\phi_2; \alpha\psi\otimes\phi=\psi\otimes(\alpha\phi)=\alpha(\psi\otimes\phi)

    此处等号就表示属于同一个等价类。

  • 第二个定义的解释

    取V有基{e1,…,en}\left\{e_{1}, \ldots, e_{n}\right\}，其对偶空间有{e∗1,…,e∗n}\left\{e^{* 1}, \ldots, e^{* n}\right\} 满足 e∗j(ei)=δije^{* j}\left(e_{i}\right)=\delta_{i}^{j}。现在，我们旋转一下，将V的基换成e~k=∑i=1nAkiei\tilde{e}_{k}=\sum_{i=1}^{n} A_{k}^{i} e_{i}。或者说，ei=∑k=1n(A−1)ike~ke_{i}=\sum_{k=1}^{n}\left(A^{-1}\right)_{i}^{k} \tilde{e}_{k}。

    我们可以知道，e~∗ℓ=∑j=1n(A−1)jℓe∗j\tilde{e}^{* \ell}=\sum_{j=1}^{n}\left(A^{-1}\right)_{j}^{\ell} e^{* j}。对偶空间基底的变化是A的逆决定的。这种变化方式与V的基底的变化方式相逆，因此称这是逆变的。

    对于V中向量v，

    ∑i=1n∑k=1nvi(A−1)ike~k=∑k=1nv~ke~k⇒v~k=∑i=1n(A−1)ikvi\sum_{i=1}^{n} \sum_{k=1}^{n} v^{i}\left(A^{-1}\right)_{i}^{k} \tilde{e}_{k}=\sum_{k=1}^{n} \tilde{v}^{k} \tilde{e}_{k} \Rightarrow\tilde{v}^{k}=\sum_{i=1}^{n}\left(A^{-1}\right)_{i}^{k} v^{i}

    其分量值的变化也是逆变的。

    对于对偶空间中向量w的分量，自然是协变（与V的基底的变化方式协同）的：w~ℓ=∑j=1nAℓjwj\tilde{w}_{\ell}=\sum_{j=1}^{n} A_{\ell}^{j} w_{j}。

    因此，我们可以写出张量的分量的变化规律来：

    t~ℓ1⋯ℓqk1⋯kp=(A−1)i1k1⋯(A−1)ipkpAℓ1j1⋯Aℓqjqtj1⋯jqi1⋯ip\tilde{t}_{\ell_{1} \cdots \ell_{q}}^{k_{1} \cdots k_{p}}=\left(A^{-1}\right)_{i_{1}}^{k_{1}} \cdots\left(A^{-1}\right)_{i_{p}}^{k_{p}} A_{\ell_{1}}^{j_{1}} \cdots A_{\ell_{q}}^{j_{q}} t_{j_{1} \cdots j_{q}}^{i_{1} \cdots i_{p}}

    考虑一个矩阵M，它是两个线性空间之间的线性映射。现在这两个空间的基底都旋转：

    e~k=∑j=1nAkjej\tilde{e}_{k}=\sum_{j=1}^{n} A_{k}^{j} e_{j} ； f~ℓ=∑i=1mBℓifi\tilde{f}_{\ell}=\sum_{i=1}^{m} B_{\ell}^{i} f_{i}

    如果我们把M的分量写成MjiM^i_j的形式，M(ej)=∑i=1mMjifiM\left(e_{j}\right)=\sum_{i=1}^{m} M_{j}^{i} f_{i}，那么

    M(e~k)=M(∑j=1nAkjej)=∑j=1nAkjM(ej)=∑j=1nAkj(∑i=1mMjifi)=∑i=1m∑j=1nMjiAkjfi=∑ℓ=1m(∑i=1m∑j=1n(B−1)iℓMjiAkj)f~ℓ\begin{aligned} M\left(\tilde{e}_{k}\right) &=M\left(\sum_{j=1}^{n} A_{k}^{j} e_{j}\right)=\sum_{j=1}^{n} A_{k}^{j} M\left(e_{j}\right)=\sum_{j=1}^{n} A_{k}^{j}\left(\sum_{i=1}^{m} M_{j}^{i} f_{i}\right) \\ &=\sum_{i=1}^{m} \sum_{j=1}^{n} M_{j}^{i} A_{k}^{j} f_{i}=\sum_{\ell=1}^{m}\left(\sum_{i=1}^{m} \sum_{j=1}^{n}\left(B^{-1}\right)_{i}^{\ell} M_{j}^{i} A_{k}^{j}\right) \tilde{f}_{\ell} \end{aligned}

    顺理成章。

    因此，M的变换方式正是（1,1）张量的变换方式，M可以认为是W⊗V∗W \otimes V^{*}的一个元素了。

  • 张量积空间的一些情形

    V∗⊗WV^{*} \otimes W和W⊗V∗W \otimes V^{*}是一样的。这就是说，ij的前后顺序没什么关系。为了理解这个事实，我们引入张量积作为向量的写法，因为张量积空间是向量空间，这是很自然的。将两个向量的张量积记成：

    a⊗b=(a1ba2b⋮an1b)a \otimes b=\left(\begin{array}{c}{a^{1} b} \\ {a^{2} b} \\ {\vdots} \\ {a^{n_{1}} b}\end{array}\right)

    现在有线性映射A:V1→W1A: V_{1} \rightarrow W_{1} and B:V2→W2B: V_{2} \rightarrow W_{2}。我们知道，A⊗BA\otimes B作用在V1V_1中元素和V2V_2中元素的张量积上，得到(A⊗B)(a⊗b)=(Aa)⊗(Bb)(A \otimes B)(a \otimes b)=(A a) \otimes(B b)。在这种记号之下，

    A⊗B=(A11BA12B⋯A1n1BA21BA22B⋯A2nB⋮⋮⋮Am11BAm12B⋯Am1n1B)A \otimes B=\left(\begin{array}{cccc}{A_{11} B} & {A_{12} B} & {\cdots} & {A_{1 n_{1}} B} \\ {A_{21} B} & {A_{22} B} & {\cdots} & {A_{2 n} B} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {A_{m_{11} B}} & {A_{m_{12}} B} & {\cdots} & {A_{m_{1 n 1}} B}\end{array}\right)

    这是很令人满意的。这种矩阵运算也叫矩阵的Kronecker积。特别的，可以想见，取M=A⊗BM=A\otimes B，取A和B的standard basis（即cartesian basis），显然有

    fi⊗e∗j=fi(ej)tf_{i} \otimes e^{* j}=f_{i}\left(e_{j}\right)^{t}

    e∗j⊗fi=fi(ej)te^{* j} \otimes f_{i}=f_{i}\left(e_{j}\right)^{t}

    （根据W⊗V∗W\otimes V^*的意思，Mjifi⊗e∗j=MM_{j}^{i} f_{i} \otimes e^{* j}=M）

    因此本节初提到的两个张量积空间是相等的。

  • 张量的缩并

    Tqp=V1⊗⋯⊗Vp⊗W1∗⊗⋯×Wq∗T_{q}^{p}=V_{1} \otimes \cdots \otimes V_{p} \otimes W_{1}^{*} \otimes \cdots \times W_{q}^{*}

    取v(i)∈Viv^{(i)} \in V_{i}，φ(j)∈Wj∗\varphi^{(j)} \in W_{j}^{*}，定义线性映射Csr:Tqp⟶Tq−1p−1C_{s}^{r}: T_{q}^{p} \longrightarrow T_{q-1}^{p-1}，那么映射

    Csr(v(1)⊗⋯⊗v(p)⊗φ(1)⊗⋯⊗φ(q))=φ(s)(v(r))v(1)⊗⋯v(r^)⋯⊗v(p)⊗φ(1)⊗⋯φ(s^)⋯⊗φ(q)C_{s}^{r}\left(v^{(1)} \otimes \cdots \otimes v^{(p)} \otimes \varphi^{(1)} \otimes \cdots \otimes \varphi^{(q)}\right)=\varphi^{(s)}\left(v^{(r)}\right) v^{(1)} \otimes \cdots v^{(\hat{r})} \cdots \otimes v^{(p)} \otimes \varphi^{(1)} \otimes \cdots \varphi^{(\hat{s})} \cdots \otimes \varphi^{(q)}

    是缩并映射。其中，带帽子的指标表示在直积中略去这一项。

  • 张量的秩

    张量积空间也是向量空间，所以张量积之间还可以继续张量积。取t∈Tqpt \in T_{q}^{p}，s∈Tsrs \in T_{s}^{r}，我们记

    Tqp×Tsr→Tqp⊗Tsr(t,s)↦t⊗s\begin{aligned} T_{q}^{p} & \times T_{s}^{r} \rightarrow T_{q}^{p} \otimes T_{s}^{r} \\(t, s) & \mapsto t \otimes s \end{aligned}

    由上一节的结论，我们可以shuffle所有那些一维的向量空间，从而得到Tqp⊗Tsr≅Tq+sp+rT_{q}^{p} \otimes T_{s}^{r} \cong T_{q+s}^{p+r}。

    授课者的remark：由此，我们可以建立张量代数T(V)=⨁p=0∞Tp(V)T(V)=\bigoplus_{p=0}^{\infty} T^{p}(V)，从而进入数学家熟悉的领域。

    令t∈Tp=V1⊗⋯⊗Vpt \in T^{p}=V_{1} \otimes \cdots \otimes V_{p}，那么定义张量秩

    rank⁡(t)=arg⁡min⁡r{r∈N∣t=∑i=1rv(i)(1)⊗⋯⊗v(i)(p), where v(i)(j)∈Vj}\operatorname{rank}(t)=\arg \min _{r}\left\{r \in \mathbb{N} | t=\sum_{i=1}^{r} v_{(i)}^{(1)} \otimes \cdots \otimes v_{(i)}^{(p)}, \text { where } v_{(i)}^{(j)} \in V_{j}\right\}

    与矩阵秩意义差不多，都是用尽可能少的秩为一的分量刻画一个线性映射。所以说一个秩为一的(p,0)张量就是p个向量的张量积（用上一节的符号写下来，还是一个向量的样子）。

    一般张量的秩的计算是NP-hard问题。常用的算法是CP（canonical polyadic） decomposition。我们之后会再提到它。张量的情况里，我们同样希望做低秩的近似。有一种叫Kruskal记号的，是这样做的：λ∈Rk\lambda \in \mathbb{R}^{k}，U(n)∈RIn×kU^{(n)} \in \mathbb{R}^{I_{n} \times k}，i=1,…,pi=1, \ldots, p，记

    [λ;U(1),…,U(p)]≡∑j=1kλju(j)(1)⊗⋯⊗u(j)(p)[\lambda ; U^{(1)}, \ldots, U^{(p)}] \equiv \sum_{j=1}^{k} \lambda_{j} u_{(j)}^{(1)} \otimes \cdots \otimes u_{(j)}^{(p)}

    InI_n是一个数列，表示每个U矩阵的行数。每个U矩阵都有k列，并且规定它们全是l2l_2-norm为1的。u(j)(i)u_{(j)}^{(i)}就是第i个U矩阵的第j列。一般来说，固定k,Y∈V1⊗⋯⊗Vp\mathcal{Y} \in V_{1} \otimes \cdots \otimes V_{p}，其中dim⁡(Vn)=In\operatorname{dim}\left(V_{n}\right)=I_{n}。然后我们找具体的λ\lambda和UU，使得Y≈X≡[λ;U(1),…,U(p)]\mathcal{Y} \approx \mathcal{X} \equiv [\lambda ; U^{(1)}, \ldots, U^{(p)}]。比如说我们熟悉的SVD就可以写成[σ;U,V][\sigma; U, V]。

    这里约等于的意思还不明确。我们通过定义张量上的距离来解决这个问题。例如，Frobenius内积

    ⟨t,s⟩F=∑i1,…,ipti1…ipsi1…ip\langle t, s\rangle_{F}=\sum_{i_{1}, \ldots, i_{p}} t^{i_{1} \ldots i_{p}} s^{i_{1} \ldots i_{p}}。

  • Tensor Embedding of Vectorial Data

    量子力学里面，人们关心张量积，是因为想要分解一个复杂系统的波函数，分离出它的自由度来。固体物理最近的一些进展使得人们产生了如下的想法：把n维欧氏空间的数据点表示成张量ti1⋯ipt^{i_{1} \cdots i_{p}}，那么

    y^=wii⋯ipti1⋯ip\hat{y}=w_{i_{i} \cdots i_{p}} t^{i_{1} \cdots i_{p}}

    就是一个predictor。这个weight tensor元素太多，一般是通过分解成低秩张量来近似求解。据这课的老师讲，那些固体物理学家盯上了一个叫TT decomposition的东西，原理是把高秩的w压缩成一些矩阵，减少需要优化的参数的数目。

    还有另外一个故事（思路），这就是把张量积空间当做是普通的线性空间，然后用我们熟悉的线性空间的工具来处理。例如，考虑一个embedding

    (xy)↦(cos⁡πx4sin⁡πx4)⊗(cos⁡πy4sin⁡πy4)∈R2⊗R2\left(\begin{array}{l}{x} \\ {y}\end{array}\right) \mapsto\left(\begin{array}{c}{\cos \frac{\pi x}{4}} \\ {\sin \frac{\pi x}{4}}\end{array}\right) \otimes\left(\begin{array}{c}{\cos \frac{\pi y}{4}} \\ {\sin \frac{\pi y}{4}}\end{array}\right) \in \mathbb{R}^{2} \otimes \mathbb{R}^{2}

    考虑一个如下图左上角的数据

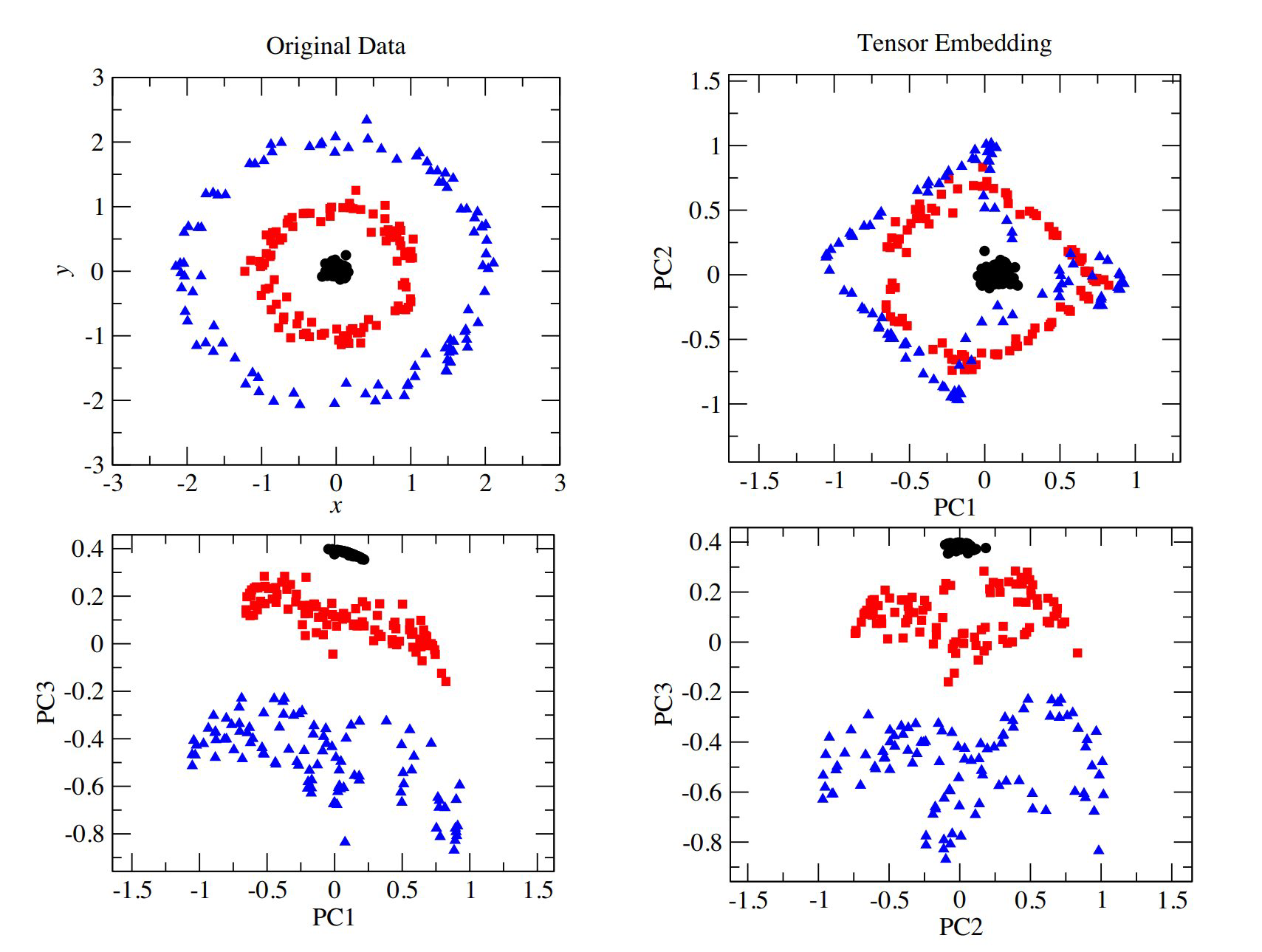
    x值接近0的点会产生向量(10)\left(\begin{array}{l}{1} \\ {0}\end{array}\right)，而x∼±1x\sim\pm1的点会产生(0±1)\left(\begin{array}{c}{0} \\ {\pm 1}\end{array}\right)。y也一样。如图下方，在张量积第1,3个分量的图中，这些点恰当地分开了。

  • Symmetric and Alternating tensors

    令πp\pi_{p}是置换群。取其元素σ\sigma，作用在Tp(V)T^{p}(V)的分量上，

    σ(t)=tiσ(1),…,iσ(p)ei1⊗⋯⊗eip\sigma(t)=t^{i_{\sigma(1)}, \ldots, i_{\sigma(p)}} e_{i_{1}} \otimes \cdots \otimes e_{i_{p}}

    如果∀σ∈πp\forall \sigma \in \pi_{p}，σ(t)=t\sigma(t)=t，那么就说这个tensor是symmetric的；如果∀σ∈πp\forall \sigma \in \pi_{p}，σ(t)=sign⁡(σ)t\sigma(t)=\operatorname{sign}(\sigma) t，那就是alternating的。所有(p,0)的symmetric 的张量的集合写作Sym⁡p(V)\operatorname{Sym}^{p}(V) 或Sp(V)S^{p}(V)，alternating的则写作⋀p(V)\bigwedge^p(V)。

  • 什么是tensor unfolding

    取t∈V1⊗⋯⊗Vpt \in V_{1} \otimes \cdots \otimes V_{p}。在分量记号下，ti1⋯ipt^{i_{1} \cdots i_{p}}所有n-th index的集合叫做第n个模。例如，取

    t=(123456)t=\left(\begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6}\end{array}\right)

    那么第一个模就是行指标1,2，第二个模就是列指标1,2,3.

    然后，固定一个mode，变化其他所有的指标，得到的就是mode-n fibre。比如说，

    令t∈V1⊗⋯⊗Vpt \in V_{1} \otimes \cdots \otimes V_p，IiI_i是ViV_i的维数。那么t的mode-n unfolding/matricization/flattening 就是一个In×(∏i≠nIi)I_{n} \times\left(\prod_{i \neq n} I_{i}\right)维的矩阵，记做t(n)\mathbf{t}_{(n)}，其中原张量分量ti1⋯ipt^{i_{1} \cdots i_{p}}被map到矩阵的第ini_n行，j列，其中

    j=1+∑ℓ=1,ℓ≠np[(iℓ−1)Jℓ]j=1+\sum_{\ell=1, \ell \neq n}^{p}\left[\left(i_{\ell}-1\right) J_{\ell}\right]

    Jℓ={∏m=ℓ+1n−1Im,ℓ≤n−21,ℓ=n−1∏r=1n−1Ir∏s=ℓ+1pIs,ℓ≥n+1J_{\ell}=\left\{\begin{array}{cl}{\prod_{m=\ell+1}^{n-1} I_{m},} & {\ell \leq n-2} \\ {1,} & {\ell=n-1} \\ {\prod_{r=1}^{n-1} I_{r} \prod_{s=\ell+1}^{p} I_{s},} & {\ell \geq n+1}\end{array}\right.

    **这玩意到底是什么意思？**我到现在也不知道。这种充满指标的公式对我来说是不可理解的。我只能拿一个性质当做定义来理解，即

    X(n)=vn(vn+1⊗⋯vp⊗v1⊗⋯vn−1)t\mathbf{X}_{(n)}=v_{n}\left(v_{n+1} \otimes \cdots v_{p} \otimes v_{1} \otimes \cdots v_{n-1}\right)^{t}

    所以说，行数是指标ini_n决定的，而至于每一列怎么排，那就是先紧着in+1i_{n+1}排，然后是in+2i_{n+2}，一直到ipi_p，再是i1i_1，然后再到in−1i_{n-1}。根据我看到的资料，这个顺序好像不是什么物理意义之类的东西决定的，而是Fortran的习惯。

  • n-mode product

    X∈V1⊗⋯⊗Vp\mathcal{X} \in V_{1} \otimes \cdots \otimes V_{p}，A=W⊗Vn∗A=W \otimes V_{n}^{*}，那么矩阵A从张量（把它想象成一个高维数阵立方体）的第n个维度上乘过去，就是

    Y≡X×nA=C1n(X⊗A)\mathcal{Y} \equiv \mathcal{X} \times_{n} A=C_{1}^{n}(\mathcal{X} \otimes A)

    从这个角度想，Y=X×nA⟺Y(n)=AX(n)\mathcal{Y}=\mathcal{X} \times_{n} A \Longleftrightarrow \mathbf{Y}_{(n)}=\mathbf{A} \mathbf{X}_{(n)}就是显然的了。如果Y=X×1U1×2U2×3⋯×pUp\mathcal{Y}=\mathcal{X} \times_{1} U_{1} \times_{2} U_{2} \times_{3} \cdots \times_{p} U_{p}，那么flattening就可以相应地写成Y(n)=UnX(n)(Un+1⊗⋯⊗Up⊗U1⊗⋯⊗Un−1)t\mathbf{Y}_{(n)}=U_{n} \mathbf{X}_{(n)}\left(U_{n+1} \otimes \cdots \otimes U_{p} \otimes U_{1} \otimes \cdots \otimes U_{n-1}\right)^{t}。

  • CP decomposition

    这玩意叫canonical，主要原因是它是从tensor rank的定义出发的。但是实际上哪怕是对矩阵这种低阶张量的分解也不是这样做的：我们是做SVD，动用一个稀疏的“core tensor”或者说singular value matrix，来分担这个矩阵在空间上多么“椭”的信息，而不是拿几个矩阵乘积加权求和去得到原矩阵（这种做法相当于使用identity作core tensor）。

    CP decomposition唯一的优势是它简单。算法上，它是这样做的：首先，定义Khatri-Rao product

    A⊙B=(A;1⊗B;1⋯A:,K⊗B:,K)A \odot B=\left(A_{; 1} \otimes B_{; 1} \cdots A_{:, K} \otimes B_{:, K}\right)

    现在有Y∈V1⊗⋯⊗Vp\mathcal{Y}\in V_{1} \otimes \cdots \otimes V_{p}，想拿X=[λ;U(1),…,U(p)]\mathcal{X}=[ \lambda ; U^{(1)}, \ldots, U^{(p)} ]去套它，判断标准采用frobenius norm。我们首先固定所有的U，只留一个U(n)U^{(n)}来优化。为了方便起见，采用unfolding出来的矩阵，这样比较好处理：

    X(n)=U(n)Λ(U(n+1)⊙⋯⊙U(p)⊙U(1)⊙⋯⊙U(n−1))t\mathbf{X}_{(n)}=U^{(n)} \Lambda\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot U^{(1)} \odot \cdots \odot U^{(n-1)}\right)^{t}

    解min⁡A∥Y(n)−A(U(n+1)⊙⋯⊙U(p)⊙U(1)⊙⋯⊙U(n−1))t∥F2\min _{A}\left\|\mathbf{Y}_{(n)}-A\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot U^{(1)} \odot \cdots \odot U^{(n-1)}\right)^{t}\right\|_{F}^{2}

    令A=U(n)ΛA=U^{(n)} \Lambda，B=(U(n+1)⊙⋯⊙U(p)⊙U(1)⊙⋯⊙U(n−1))B=\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot\right.\left.U^{(1)} \odot \cdots \odot U^{(n-1)}\right)

    那么就可以用MP伪逆求得

    A(BtB)=Y(n)B⇒A=Y(n)B(BtB)+A\left(B^{t} B\right)=\mathbf{Y}_{(n)} B \Rightarrow A=\mathbf{Y}_{(n)} B\left(B^{t} B\right)^{+}

    那么，λ\lambda就是A的每一列的模，U(n)U^{(n)}就是A的每一列归一化之后得到的矩阵。

    如此这般，先随机搞一批U，然后一个一个地优化。这个方法很令人不舒服，因为它是ill-posed的，不能保证收敛。

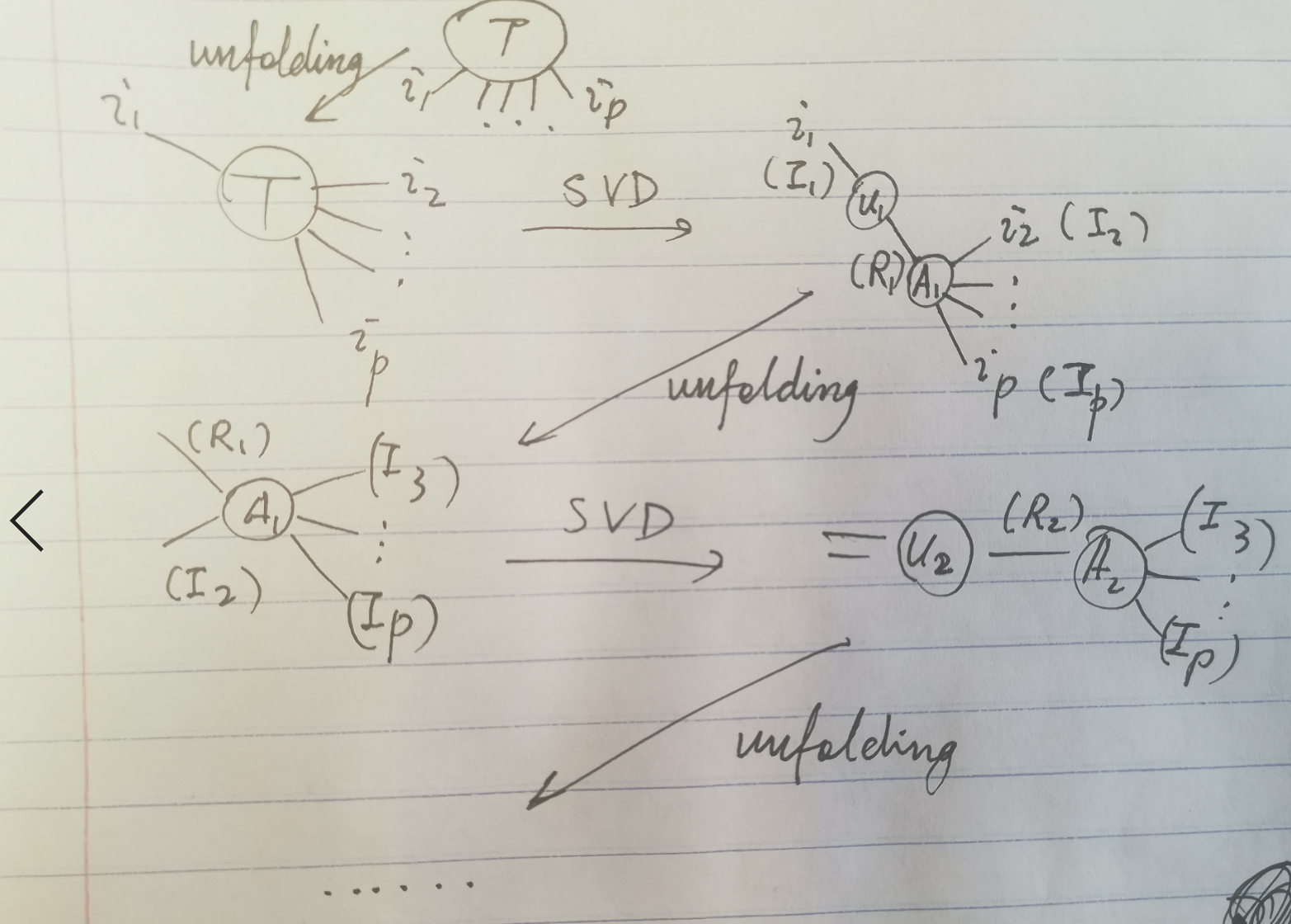
  • HOSVD（high order SVD）

    这是低维的SVD在高维的推广，也叫tucker decomposition，但tucker本人只是搞了三维的情况。现在令InI_n是每个VnV_n的维数，那么X∈V1⊗⋯⊗Vp≡Tp\mathcal{X} \in V_{1} \otimes \cdots \otimes V_{p} \equiv T^{p}可以被分解成

    X=S×1U(1)×2U(2)⋯×pU(p)\mathcal{X}=\mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \cdots \times_{p} U^{(p)}

    比如说，对于一个矩阵，M=Σ×1U×2VM=\Sigma\times_1U\times_2 V。

    我个人理解这个S是sparse，不是singular。可能是因为我从来就没理解singular value这个名字到底啥意思。sparse不仅是说S“只有对角元”，也说明这个新东西参数少。还是拿矩阵的SVD来说，本来T的维数是m×nm\times n，现在有k≪m,nk\ll m,n个奇异值，那么只需要k(m+n−1)≪mnk(m+n-1)\ll mn个参数就能刻画整个矩阵。

    这个S也满足矩阵的奇异值分解的诸般性质。比如

    • U(n)=(U(1)(n)⋯U(In)(n))U^{(n)}=\left(U_{(1)}^{(n)} \cdots U_{\left(I_{n}\right)}^{(n)}\right)是In×InI_{n} \times I_{n}的正交矩阵；
    • ∀n∈{1,…,p},⟨Sin=α,Sin=β⟩F=0\forall n \in\{1, \ldots, p\},\left\langle S^{i n=\alpha}, S^{i_{n}=\beta}\right\rangle_{F}=0 for α≠β\alpha \neq \beta，S的“列”互相正交；
    • ∥Sin=1∥F≥⋯≥∥Sin=In∥F≥0\left\|S^{i_{n}=1}\right\|_{F} \geq \cdots \geq\left\|S^{i_{n}=I_{n}}\right\|_{F} \geq 0，S的“列”可以排序。

    怎么求这个分解呢？我们可以对unfolding得到的矩阵做SVD：

    X(n)=U(n)Σ(n)V(n)t\mathbf{X}_{(n)}=U^{(n)} \Sigma^{(n)} V^{(n)^{t}}

    顺手排序：

    σ1(n)≥σ2(n)⋯≥σIn(n)≥0\sigma_{1}^{(n)} \geq \sigma_{2}^{(n)} \cdots \geq \sigma_{I_{n}}^{(n)} \geq 0

    然后用这个U(i)U^{(i)}定义

    S=X×1U(1)t×2U(2)t⋯×pU(p)tS=\mathcal{X} \times_{1} U^{(1)^{t}} \times_{2} U^{(2) t} \cdots \times_{p} U^{(p)^{t}}

    这样就都求出来了。这样得到的结果自然满足以上性质，例如后两条（第一条是平凡的）

    S(n)=U(n)tX(n)(U(n+1)t⊗⋯⊗U(p)t⊗U(1)t⊗⋯⊗U(n−1)t)t=U(n)tX(n)(U(n+1)⊗⋯⊗U(p)⊗U(1)⊗⋯⊗U(n−1))=Σ(n)V(n)t(U(n+1)⊗⋯⊗U(p)⊗U(1)⊗⋯⊗U(n−1))\begin{aligned} \mathbf{S}_{(n)} &=U^{(n) t} \mathbf{X}_{(n)}\left(U^{(n+1)^{t}} \otimes \cdots \otimes U^{(p) t} \otimes U^{(1)^{t}} \otimes \cdots \otimes U^{(n-1)^{t}}\right)^{t} \\ &=U^{(n)^{t}} \mathbf{X}_{(n)}\left(U^{(n+1)} \otimes \cdots \otimes U^{(p)} \otimes U^{(1)} \otimes \cdots \otimes U^{(n-1)}\right) \\&=\Sigma^{(n)} V^{(n)^{t}}\left(U^{(n+1)} \otimes \cdots \otimes U^{(p)} \otimes U^{(1)} \otimes \cdots \otimes U^{(n-1)}\right)\end{aligned}

    从这里能看出来，那一串U是正交变换，所以S的orthogonality是V决定的，V自然满足这性质。然后∥Sin=1∥F=σ1(n)\left\|S^{i_{n}=1}\right\|_{F}=\sigma_1^{(n)}，以此类推，所以排序必然成立。这样，所有性质都满足。

  • TTSVD

    所谓Tensor Train SVD，指的是把张量的每个分量用一连串矩阵相乘的形式表示的操作。附图中，TTSVD的记号长得像一列火车，因此得名。我对这个东西的理解不是很好，所以简要记之，以后再想。

    A(i1,i2,…,ip)=G1(i1)G2(i2)…Gp(ip)A\left(i_{1}, i_{2}, \ldots, i_{p}\right)=G_{1}\left(i_{1}\right) G_{2}\left(i_{2}\right) \ldots G_{p}\left(i_{p}\right)

    其中Gk(ik)G_{k}\left(i_{k}\right) 是 Rk−1×RkR_{k-1} \times R_{k}的一族矩阵（换句话说，GkG_k是一个VRk−1⊗VRk⊗VIkV^{R_{k-1}}\otimes V^{R_k}\otimes V^{I_k}的张量）。由“边界条件”，r0=rp=0r_0=r_{p}=0。算法是这样的：从i1i_1这维度unfold，做SVD，然后得到U1U_1，这是一个1×I1×R11\times I_1\times R_1的数阵。接着，对SVD右面的ΣV\Sigma V部分做unfolding，同时unfoldr1r_1和i2i_2两个维度，再做SVD，得到U2U_2，这是一个(R1×I2)×R2(R_1\times I_2)\times R_2的矩阵……通过这种方式，我们就可以从UU得出GG来。

(三种decomposition方法的图示)

(tensor train SVD细节)